23．(12分)如图，已知二次函数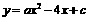的图像经过点A和点B．

(1)求该二次函数的表达式；

(2)写出该抛物线的对称轴及顶点坐标；

(3)点P(m，m)与点Q均在该函数图像上(其中m＞0)，且这两点关于抛物线的对称轴对称，求m的值及点Q 到x轴的距离．

22．(10分)已知：如图1，AB⊥BD，CD⊥BD，垂足分别为B、D，AD和BC相交于点E，EF⊥BD，垂足为F，我们可以证明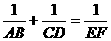成立(不要求考生证明).若将图1中的垂线改为斜交，如图2，AB∥CD，AD，BC相交于点E，过点E作EF∥AB，交BD于点F，则：

⑴　　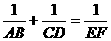　 还成立吗？如果成立，请给出证明；

如果不成立，请说明理由；

⑵　　　 请找出S_△ABD，S_△BED和S_△BDC间的关系式，并给出证明.

21. (12分)有一种葡萄，从树上摘下来以后不保鲜最多只能存放一周，如果放在冷藏室，可以延长保鲜时间，但每天仍有一定数量的葡萄变质。设保鲜期内的个体重量基本保持不变，现有经营者，按市场价收购了这种葡萄200千克，如果市场价此时是每千克2元，据估计，此后每天每千克葡萄价格会上涨0.2元，但存放一天需要各种费用20元，平均每天还有一千克变质丢弃。

(1)设x天后每千克葡萄的价格为p元，写出p与x之间的函数关系式。

(2)若存放x天后将葡萄一次性售出，设销售总金额为y元，写出y与x之间的函数关系式。

(3)该经营者将这批葡萄存放多少天后售出，可以获得最大利润，最大利润是多少？

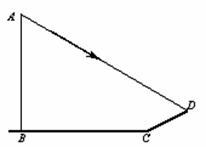
20．(10分)如图:学校旗杆附近有一斜坡．小明准备测量学校旗杆AB的高度，他发现当斜坡正对着太阳时，旗杆AB的影子恰好落在水平地面和斜坡的坡面上，此时小明测得水平地面上的影长BC=20米，斜坡坡面上的影长CD=8米，太阳光线AD与水平地面成30°角，斜坡CD与水平地面BC成30°的角，求旗杆AB的高度．

19．(10分)已知，如图，AB和DE是直立在地面上的两根立柱.AB=5m，某一时刻AB在阳光下的投影BC=3m.

(1)请你在图中画出此时DE在阳光下的投影；

(2)在测量AB的投影时，同时测量出DE在阳光下的投影长为6m，请你计算DE的长.

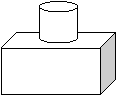
18．(6分)画出下面实物的三视图：

17．计算(6分)： 6tan² 30°－sin 60°－2sin 45°

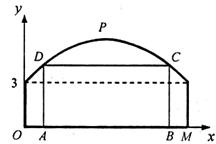
24．(本题满分9分)如图，某隧道横截面的上下轮廓线分别由抛物线中对称的一部分和矩形的一部分构成，最大高度为6米，底部宽度为12米．现以O点为原点，OM所在直线为x轴建立直角坐标系．

　 (1)直接写出点M及抛物线顶点P的坐标；

　 (2)求出这条抛物线的函数解析式；

　 (3)若要搭建一个矩形“支撑架”AD-DC-CB，使C、D点在抛物线上，A、B点在地面OM上，则这个“支撑架”总长的最大值是多少?

23．(本题满分9分)如图，抛物线y=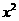+bx+c经过A(一，0)、B(O，一3)两点，

　 　此抛物线的对称轴为直线，，顶点为C，且，与直线AB交于点D．

　　(1)求此抛物线的解析式；

　 　(2)直接写出此抛物线的对称轴和顶点坐标；

(3)连接BC，求证：BC=DC．

22．(本题满分9分)某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品的售价每上涨l元，则每个月少卖l0件(每件售价不能高于65元)．设每件商品的售价上涨x元(x为正整数)，每个月的销售利润为y元．

(1)求y与z的函数关系式并直接写出自变量x的取值范围；

(2)每件商品的售价定为多少元时，每个月可获得最大利润?最大的月利润是多少元?

(3)每件商品的售价定为多少元时，每个月的利润恰为2200元?根据以上结论，请你直接写出售价在什么范围时，每个月的利润不低于2200元?