4．解：根据勾股定理得直角三角形得另一条直角边为：

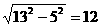，所以地毯的总长度是5+12＝17(米)，

面积为17×2＝34(米²)，总价钱为34×18＝612(元)

答：铺万这个楼道要用612元。

3．解：根据勾股定理得，蔬菜大棚的斜面的宽度即直角三角形的斜边长为：

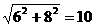　m，所以蔬菜大棚的斜面面积为：10×20＝200m²。

答：阳光透过的最大面积为200平方米。

2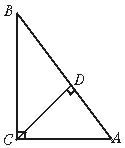．解：(1)∵△ABC中，∠C=90°，AC=2.1 cm，BC=2.8 cm

∴AB²=AC²+BC²=2.1²+2.8²=12.25

∴AB=3.5 cm

∵S_△ABC=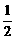AC·BC=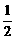AB·CD

∴AC·BC=AB·CD

∴CD=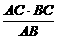==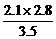1.68(cm)

(2)在Rt△ACD中，由勾股定理得：

AD²+CD²=AC²

∴AD²=AC²－CD²=2.1²－1.68²

=(2.1+1.68)(2.1－1.68)

=3.78×0.42=2×1.89×2×0.21

=2²×9×0.21×0.21

∴AD=2×3×0.21=1.26(cm)

∴BD=AB－AD=3.5－1.26=2.24(cm)

1．解：∵AD⊥AB，∴△ABD是直角三角形。

根据勾股定理得：AD²+AB²=BD²，即3²+4²＝BD²， ∴BD=5；

同理在△DBC中，∵BD⊥BC，∴CD²=BD²+BC²，

即：CB²=13²－5²＝144，∴CB=12

1．169　　 2．8　 3．7　　 4．3、4、5；　 5．250　　 6．6、8　　 7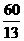．　　 8．12

8．A　 9．B 将等式两边整理的a²+b²＝c²，所以是直角三角形。10．C梯子的长度不变，两次利用勾股定理可得答案选C

1．D 根据勾股定理的，直角所对的边是斜边。 2．A　 3．C 利用轴对称易知，30°角所对的直角边是斜边的一半，由勾股定理知，另一边是选C .4．C　 本题的三角形有锐角三角形与钝角三角形两种情况，当是锐角三角形是周长是42；当是钝角三角形时是周长是32　　 5．B　 6．D　 7．A 边长为4、6的等腰三角形有4、4、6与4、6、6两种情况，当是4、4、6时，底边上的高为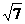；当是4、6、6时，底边上的高是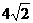，所以选A

5．甲、乙两位探险者到沙漠进行探险，没有了水，需要寻找水源．为了不致于走散，他们用两部对话机联系，已知对话机的有效距离为15千米．早晨8：00甲先出发，他以6千米/时的速度向东行走，1小时后乙出发，他以5千米/时的速度向北行进，上午10：00，甲、乙二人相距多远？还能保持联系吗？

4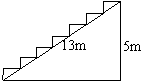．如图，某购物中心在会十.一间准备将高5 m,长13m，宽2m的楼道上铺地毯,已知地毯每平方米18元，请你帮助计算一下，铺完这个楼道至少需要多少元钱?