
题目列表(包括答案和解析)
2.若关于x的方程 的解为x=
的解为x=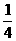 ,则m
.
,则m
.
1.当x= 时, 与
与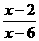 相等.
相等.
3. 无解,则m的值是( )
无解,则m的值是( )
A.-2 B.2 C.3 D.-3
2.A、B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程( )
A.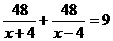 B.
B. C.
C. D.
D.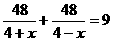
1.方程 的根是( )
的根是( )
A. B.0 C.2 D.3
B.0 C.2 D.3
2. 如图所示,某人到岛上去探宝,从A处登陆后先往东走4km,又往北走1.5km,遇到障碍后又往西走2km,再折回向北走到4.5km处往东一拐,仅走0.5km就找到宝藏。问登陆点A与宝藏埋藏点B之间的距离是多少?
如图所示,某人到岛上去探宝,从A处登陆后先往东走4km,又往北走1.5km,遇到障碍后又往西走2km,再折回向北走到4.5km处往东一拐,仅走0.5km就找到宝藏。问登陆点A与宝藏埋藏点B之间的距离是多少?
解:如图,过点B作BC⊥AD于C,则AC=2.5,BC=6,
由勾股定理求得AB=6.5(km)
1.解:根据题意得:Rt△ADE≌Rt△AEF
∴∠AFE=90°,AF=10 cm,EF=DE
设CE=x cm,则DE=EF=CD-CE=8-x
在Rt△ABF中由勾股定理得:
AB2+BF2=AF2,即82+BF2=102,
∴BF=6 cm
∴CF=BC-BF=10-6=4(cm)
在Rt△ECF中由勾股定理可得:
EF2=CE2+CF2,即(8-x)2=x2+42
∴64-16x+x2=x2+16
∴x=3(cm),即CE=3 cm
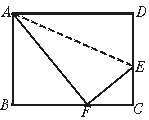
1.如图3,已知长方形ABCD中AB=8 cm,BC=10 cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求CE的长.
6.解:本题中虽然给出了直角三角形的两边是3、4,而没有指出它们一定是直角边或斜边,所以本题应该分情况讨论。
(1)当3、4,是直角边时,第三边等于
(2)当3与所求的第三边时直角边,4是斜边时,第三边等于
所以本题的答案应该是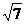 或5。
或5。
备用题:
5.解:如图,甲从上午8:00到上午10:00一共走了2小时,
 走了12千米,即OA=12.
走了12千米,即OA=12.
乙从上午9:00到上午10:00一共走了1小时,
走了5千米,即OB=5.
在Rt△OAB中,AB2=122十52=169,∴AB=13,
因此,上午10:00时,甲、乙两人相距13千米.
∵15>13, ∴甲、乙两人还能保持联系.
答:上午10:00甲、乙两人相距13千米,两人还能保持联系.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com