
题目列表(包括答案和解析)
8.
一种胸花图案的制作过程如图1-图3,图1中每个圆的半径均为1,将图2绕点O逆时针旋转 得到图2,再将图2绕点O逆时针旋转
得到图2,再将图2绕点O逆时针旋转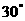 得到图3,则图3中实线的长为( )
得到图3,则图3中实线的长为( )

A.  B.
B. C.
C.
 D.
D.

7.
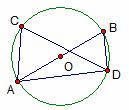
 如图,A、B、C三点在正方形网络线的交点处,若将
如图,A、B、C三点在正方形网络线的交点处,若将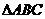 绕着点A逆时针旋转得到
绕着点A逆时针旋转得到 ,则
,则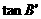 的值为( )
的值为( )
A. 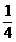 B.
B.

C. 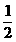 D.
D. 
6.
二次函数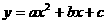 的图象如图所示,则下列说法正确的是( )
的图象如图所示,则下列说法正确的是( )
A. 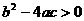 B.
B.

C. 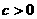 D.
D.
5.
如图,AB是⊙ 的直径,CD是⊙
的直径,CD是⊙ 的弦,若
的弦,若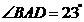 ,则
,则 的大小为( )
的大小为( )
A.  B.
B.

 C.
C.
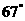 D.
D.

4.
 抛物线
抛物线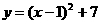 的顶点坐标为( )
的顶点坐标为( )
A.(7,1) B.(1,7) C.(-1,7) D.(1,-7)
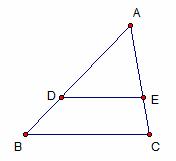
3. 如图,在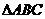 中,D、E两点分别在AB、AC边上,
中,D、E两点分别在AB、AC边上,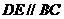 若
若 ,则
,则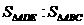 为( )
为( )
A.  B.
B.
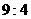 C.
C.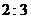 D.
D.
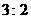
2. 将抛物线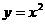 平移得到抛物线
平移得到抛物线 ,叙述正确的是( )
,叙述正确的是( )
 A.向上平移5个单位 B.向下平移5个单位
A.向上平移5个单位 B.向下平移5个单位
C.向左平移5个单位 D.向右平移5个单位
1. 下列图形中是轴对称的图形是( )

1解(1)原式= =12
=12
(2)原式= .
.
 2解:本题主要考查学生运用平移和旋转的性质进行作图的能力.如图所示.
2解:本题主要考查学生运用平移和旋转的性质进行作图的能力.如图所示.
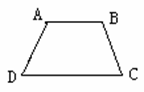
3解:甲、乙、丁三位同学的条件均符合要求.
理由:甲从同一底上的两个角进行限定;乙则从对角及邻角之间的关系进行限定,
由于AB∥CD,故∠B+∠C=180°,从而可由∠B+∠D=180°,得∠C=∠D;丁则从对称性进行限定,这些条件都能使梯形ABCD成为等腰梯形.
对于丙的限定,由于∠A+∠D=180°,故∠A=∠D=90°,从而梯形ABCD是直角梯形.
可另外添加∠C=∠D.
4解:(1)猜想AB1∥CB.
 因为△ABC为等腰三角形,所以,由旋转性质知AC=AC1,且△AB1C1也是等腰三角形,所以AB=BC=AB1=B1C.,∠ACB=∠AC1B1=∠B1AC1.
B1
因为△ABC为等腰三角形,所以,由旋转性质知AC=AC1,且△AB1C1也是等腰三角形,所以AB=BC=AB1=B1C.,∠ACB=∠AC1B1=∠B1AC1.
B1
由AC=AC1,得∠AC1C=∠ACB,知∠B1AC1=∠AC1C,所以AB1∥CB.
(2)当∠C=600时,△ABC为等边三角形,同理可得AB1∥CB.
(3)当∠C<600时,如图6所示,同理可得AB1∥CB.
5解:(1)因为MN∥BC,所以∠OEC=∠ECB,∠OFC=∠FCD.又因为CE平分∠ACB,FC平分∠ACD.所以∠ECB=∠OCE,∠OCF=∠FCD,所以∠OEC=∠OCE,∠OFC=∠OCF,所以EO=OC,FO=OC,故EO=FO;
(2)由(1)知,OE=OC=OF,当OC=OA,即点O为AC的中点时,有OE=OC=OF=OA,这时四边形AECF是矩形;
(3)由正方形AECF可知,AC⊥EF,又由于EF∥BC,得∠ACB=90°,所以△ABC是∠ACB=90°的直角三角形.
6解:分两种情况讨论:①若以 为底,
为底, 为腰,则如图3,在
为腰,则如图3,在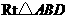 和
和 中,分别由勾股定理,得
中,分别由勾股定理,得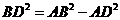
 ,
,

 即
即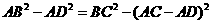 ,所以
,所以
 ,即
,即 ,所以
,所以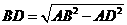 =
=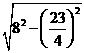 =
= ;②若以
;②若以 为底,
为底, 为腰,则如图4,在
为腰,则如图4,在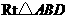 和
和 中,分别由勾股定理,得
中,分别由勾股定理,得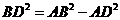
 ,即
,即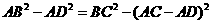 ,所以
,所以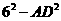
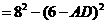 ,即
,即 ,所以
,所以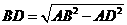 =
= =
=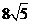 .
.
6.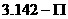 7.17 8.6
9.18 10.等腰或直角或等腰直角三角形
7.17 8.6
9.18 10.等腰或直角或等腰直角三角形
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com