
题目列表(包括答案和解析)
1.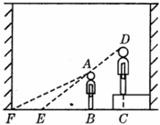 如图1所示,课堂上小亮站在座位上回答数学老师提出的问题,那么数学老师观察小亮身后,盲区是( )
如图1所示,课堂上小亮站在座位上回答数学老师提出的问题,那么数学老师观察小亮身后,盲区是( )
A.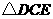 B.四边形
B.四边形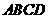
C. D.
D.
22.
已知: ,
,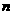 是方程
是方程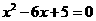 的两个实数根,且
的两个实数根,且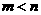 ,
,
抛物线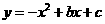 的图象经过点A(
的图象经过点A( ),B(
),B(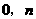 ).
).
(1) 求这个抛物线的解析式;
(2)
设(1)中的抛物线与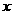 轴的另一交点为C,抛物线的顶点为D,试求出点C,D的坐标
轴的另一交点为C,抛物线的顶点为D,试求出点C,D的坐标
和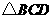 的面积;(注:抛物线
的面积;(注:抛物线
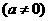 的顶点坐标为
的顶点坐标为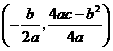 );
);

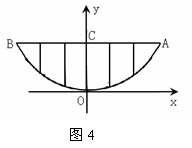
21.某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图4所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.以O为原点,OC所在的直线为y轴建立平面直角坐标系,请根据以上的数据,求出抛物线y=ax2的解析式;
17,求函数y=4x2+24x+35;的图像的对称轴、顶点坐标及与x轴的交点坐标.
18,已知抛物线C1的解析式是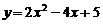 ,抛物线C2与抛物线C1关于x轴对称,求抛物线C2的解析式.
,抛物线C2与抛物线C1关于x轴对称,求抛物线C2的解析式.
19,已知抛物线y=x2-2x-8.
(1)试说明该抛物线与x轴一定有两个交点.
(2)若该抛物线与x轴的两个交点分别为A、B(A在B的左边),且它的顶点为P, 求△ABP的面积.
20.已知:如图3,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上, 分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.
(1)用含y的代数式表示AE.
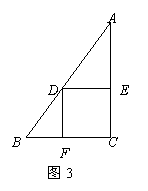 (2)求y与x之间的函数关系式,并求出x的取值范围.
(2)求y与x之间的函数关系式,并求出x的取值范围.
(3)设四边形DECF的面积为S,求出S的最大值.
9,二次函数y=-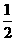 2x2+3的开口方向是_________.
2x2+3的开口方向是_________.
10,抛物线y=x2+8x-4与直线x=4的交点坐标是__________.
11,若二次函数y=ax2的图象经过点(-1,2),则二次函数y=ax2的解析式是__
12,已知抛物线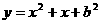 经过点
经过点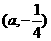 和
和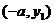 ,则
,则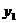 的值是 .
的值是 .
13,已知二次函数y=ax2+bx+c的图象与x轴交于A(1,0),B(3,0)两点,与y轴交于点
C (0,3),则二次函数的解析式是 .
14,若函数y=3x2与直线y=kx+3的交点为(2,b),则k=__,b=__.
15,函数y=9-4x2,当x=_________时有最大值________.
16,两数和为10,则它们的乘积最大是_______,此时两数分别为________.
1,已知点(a,8)在二次函数y=a x2的图象上,则a的值是( )
A,2 B,-2 C,±2 D,±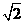
2,抛物线y=x2+2x-2的图象最高点的坐标是( )
A.(2,-2) B.(1,-2) C.(1,-3) D.(-1,-3)
3,若y=(2-m) 是二次函数,且开口向上,则m的值为( )
是二次函数,且开口向上,则m的值为( )
A.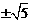 B.-
B.-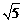 C.
C.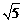 D.0
D.0
4,二次函数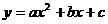 的图象如图1所示,则下列结论正确的是( )
的图象如图1所示,则下列结论正确的是( )
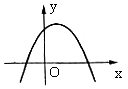 A.
A. 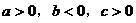 B.
B. 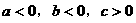
C. 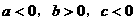 D.
D. 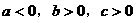
|
5,如果二次函数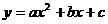 (a>0)的顶点在x轴上方,那么( )
(a>0)的顶点在x轴上方,那么( )
A,b2-4ac≥0 B,b2-4ac<0 C,b2-4ac>0 D,b2-4ac=0
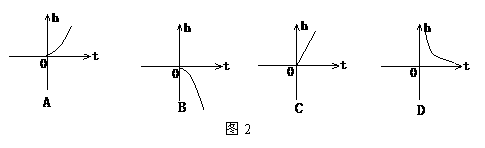 6,已知h关于t的函数关系式为h=
6,已知h关于t的函数关系式为h=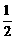 gt2(g为正常数,t为时间), 则如图2中函数的图像为( )
gt2(g为正常数,t为时间), 则如图2中函数的图像为( )
7,已知二次函数y=-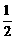 x2-3x-
x2-3x-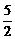 ,设自变量的值分别为x1,x2,x3,且-3<x1<x2<x3,
则对应的函数值y1,y2,y3的大小关系是( )
,设自变量的值分别为x1,x2,x3,且-3<x1<x2<x3,
则对应的函数值y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y1<y2<y3; C.y2>y3>y1 D.y2<y3<y1
8,关于二次函数y=x2+4x-7的最大(小)值,叙述正确的是( )
A.当x=2时,函数有最大值 B.x=2时,函数有最小值
C.当x=-1时,函数有最大值 D.当x=-2时,函数有最小值
21.正方形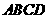 边长为4,
边长为4, 、
、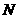 分别是
分别是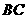 、
、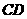 上的两个动点,当
上的两个动点,当 点在
点在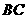 上运动时,保持
上运动时,保持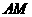 和
和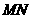 垂直,
垂直,
(1)证明: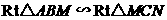 ;
;
(2)设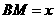 ,梯形
,梯形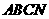 的面积为
的面积为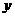 ,求
,求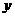 与
与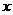 之间的函数关系式;当
之间的函数关系式;当 点运动到什么位置时,四边形
点运动到什么位置时,四边形 面积最大,并求出最大面积;
面积最大,并求出最大面积;
(3)当 点运动到什么位置时
点运动到什么位置时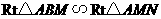 ,并求
,并求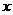 的值.
的值.


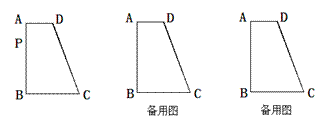
20.直角梯形ABCD中,AD∥BC,∠B=90°, AB=7,AD=2,BC=3,在腰AB上有一动点P.
(1)连接DP、CP,使得△PAD与△PBC相似,求出此时AP的长;
(2)若点P在直线AB上运动则满足上述条件的P共有_____________个;
(3)在直线AB上存在一点M,使得△DMC周长最小,直接写出AM的长与△DMC的周长。
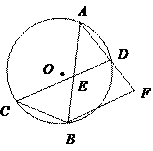
19.如图,⊙ 中,弦
中,弦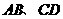 相交于
相交于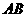 的中点
的中点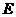 ,连接
,连接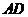 并延长至点
并延长至点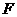 , 使
, 使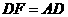 ,连接BC、
,连接BC、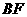 .
.
(1)求证: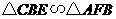 ;(2)当
;(2)当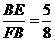 时,求
时,求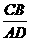 的值.
的值.
18.如图,已知抛物线与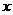 交于A(-1,0)、E(3,0)两点,与
交于A(-1,0)、E(3,0)两点,与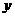 轴交于点B(0,3)。
轴交于点B(0,3)。
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积;
(3)△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com