6、已知圆锥的底面半径为9cm，母线长为10cm，则圆锥的全面积是　　　　　　　 cm²

5、点P关于原点对称的点Q的坐标是(-1，3)，则P的坐标是　　　　　　　　　　　

4、成语“水中捞月”用概率的观点理解属于不可能事件，请你仿照它写出一个必然事件

　 　　　　　　　　　　　　　　　　　　。

3、若关于x的一元二次方程(a+1)x²+4x+a²-1=0的一根是0，则a＝　　　　　　 　。

2、计算＝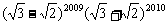　　　　　　　　　　

1、已知式子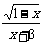有意义，则x的取值范围是　　　　　　　

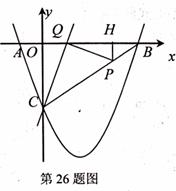
26．(12分)如图，已知抛物线与坐标轴交于A、B、C三点，　 A点的坐标为(-1，0)，过点C的直线与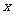轴交于点Q，点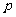是线段BC上的一个动点，过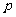作PH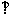OB于点H，若PB=5t，且。

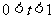(1)填空：点C的坐标是_______，b=_______，c=_______；

(2)求线段QH的长(用含t的式子表示)；

(3)依点P的变化，是否存在t的值，使以P、H、Q为顶点的三角形与△COQ相似?若存在，求

出所有t的值：若不存在，说明理由。

25．(12分)如图(1)，小明将一张矩形纸片沿对角线剪开，得到两张三角形纸片(如图(2))，量得他们的斜边长为10cm，较小锐角为30。，再将这两张三角纸片摆成如图(3)的形状，但点B、C、F、D在同一条直线上，且点C与点F重合(在图(3)至图(6)中统一用F表示)

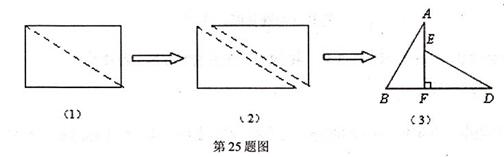
小明在对这两张三角形纸片进行如下操作时遇到了三个问题，请你帮助解决。

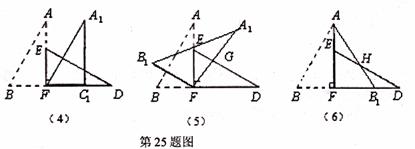
(1)将图(3)中△ABF？沿BD向右平移到图(4)的位置，使点B与点F重合，请你求山平移的距离；

(2)将图(3)中△ABF绕点F顺时针方向旋转30。到图(5)的位置，A．F交DE于点G，请你求出线段FG的K度； 　

(3)将图(3)中的△ABF沿直线AF翻折到图(6)的位置，AB，交DE丁点H，请证明：AH=DH。

24．(12分)某商品的进价为每件40元．当售价为每件60元时，每星期可卖出300件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出20件．在确保盈利的前提下，解答下列问题：

(1)若设每件降价x元、每星期售出商品的利润为y元，请写山y与x的函数关系式，并求出自

变量x的取值范围；

(2)当降价多少元时，每星期的利润最大?最大利润是多少?

23．(10分)如图，AB是⊙O直径，OD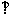弦BC丁点F，且交⊙O于点E，若∠AEC=∠0DB．

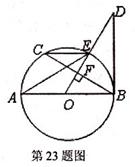(1)判断直线BD和o(二)的位置关系，并给出证明；

(2)当AB=10，BC=8时，求BD的长。