24．(8分)有一种螃蟹，从海上捕获后不放养，最多只能存活两天，如果放养在塘内，可以延长存活时间，但每天也有一定数量的蟹死去，假设放养期内蟹的个体重量基本保持不变。现有一经销商，按市场价收购了这种活蟹1000千克放养在塘内，此时市场价为每千克30元。据测算，此后每千克活蟹的市场价每天可上升1元，但放养一天需各种费用400元，且平均每天还有10千克蟹死去，假定死蟹均于当天全部售出，售价是每千克20元。

(1)设x天后每千克活蟹的市场价为P元，写出P关于x的函数关系式；

(2)如果放养x天后将活蟹一次性出售，并记1000千克蟹的销售总额Q元，写出Q关于x的函数关系式；

(3)该经销商将这批蟹放养多少天后出售，可获得最大利润(利润=销售总额－收购成本－费用)？最大利润是多少

23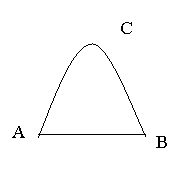．(8分)某工厂大门是一抛物线水泥建筑物(如图)，大门地面宽AB= 4米，顶部C离地面高为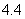米，现有一辆载满货物的汽车欲通过大门，货物顶点距地面米，装货宽度为米，请通过计算，判断这辆汽车能否顺利通过大门？

22．(8分)根据下列条件，求二次函数的关系式：

(1)抛物线经过点(0，3)、(1，0)、(3，0)；

(2)抛物线顶点坐标是(-1，-2)，且经过点(1，10)。

21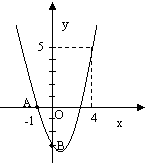．(7分)如图二次函数y=ax²+bx+c的图象经过A 、B、C三点，　 C

(1)观察图象，写出A 、B、C三点的坐标，并求出抛物线解析式，

(2)求此抛物线的顶点坐标和对称轴

(3)观察图象，当x取何值时，y<0？y=0？y>0?

20．(7分)已知二次函数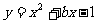的图象经过点(3，2)。

(1)求这个二次函数的关系式；

(2)画出它的图象，并指出图象的顶点坐标；

(3)当x＞0时，求使y≥2的x的取值范围。

19．如图，某农场要盖一排三间长方形的羊圈，打算一面利用旧墙，其余各面用木材围成栅栏，该计划用木材围成总长24m的栅栏，设每间羊圈的一边长为x (m)，三间羊圈的总 面积s (m²),则s关于x的函数关系式是______________,x的取值范围_________,当x=_________时，s最大.

18．已知抛物线的开口向上，并且以y轴为对称轴，试写出这条抛物线的关系式(任写两个)　　　　　　　 、　　　　　　　　　　　 。

17．已知抛物线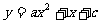与x轴交点的横坐标为 –1，则=　　　 。

16．有一长方形条幅，长为a m，宽为b m，四周镶上宽度相等的花边，求剩余面积S(m²)与花边宽度x(m)之间的函数关系式为　　　　　　　 ，自变量x的取值范围为　　　　 。

15．抛物线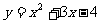与y轴的交点坐标是　　 　，与x轴的交点坐标是　　　　 。