4．抛物线y=2x²如何平移可得到抛物线y=2(x－4)²－1(　 )

　　 A．向左平移4个单位，再向上平移1个单位;

　　 B．向左平移4个单位，再向下平移1个单位;

　　 C．向右平移4个单位，再向上平移1个单位;

　　 D．向右平移4个单位，再向下平移1个单位

3．若直线y=3x+m经过第一、三、四象限，则抛物线y=(x－m)²+1的顶点必在(　 )

　　 A．第一象限　 B．第二象限　 C．第三象限　 D．第四象限

2．一台机器原价为60万元，如果每年的折旧率为x，两年后这台机器的价位为y万元，则y与x之间的函数表达式为(　 )

　 A．y=60(1－x)²　 B．y=60(1－x)　 C．y=60－x²　 D．y=60(1+x)²

1．与抛物线y=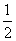－x²+3x－5的形状、开口方向都相同，只有位置不同的抛物线是(　 )

　　 A．y=x²+3x－5　　 B．y=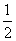－x²+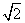x 　　C．y=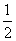x²+3x－5　 D．y=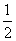x²

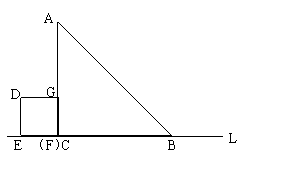
28．(12分)如图，在△ABC中，∠ACB=90°AC=BC=6㎝，正方形DEFG的边长为2㎝，其一边EF在BC所在的直线L上，开始时点F与点C重合，让正方形DEFG沿直线L向右以每秒1㎝的速度作匀速运动，最后点E与点B重合.

⑴请直接写出该正方形运动6秒时与△ABC重叠部分面积的大小；

⑵设运动时间为x(秒)，运动过程中正方形DEFG与△ABC重叠部分的面积为y(㎝²).

①在该正方形运动6秒后至运动停止前这段时间内，求y与x之间的函数关系式；

②在该正方形整个运动过程中，求当x为何值时，y=.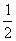

27．一条隧道的截面如图所示，它的上部是一个以AD为直径的半圆O，下部是一个矩形ABCD．

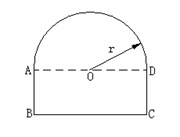(1)当AD＝4米时，求隧道截面上部半圆O的面积；

(2)已经矩形ABCD相邻两边之和为8米，半圆O的半径为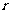米．

①求隧道截面的面积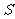(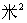)关于半径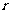(米)的函数关系式(不要求写出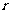的取值范围)；

②若2米≤CD≤3米，利用函数图象求隧道截面的面积S的最大值(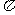取3.14，结果精确到0.1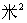)(12分)

26、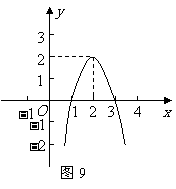二次函数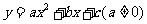的图象如图9所示，根据图象解答下列问题：(8分)

(1)写出方程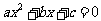的两个根．

(2)写出不等式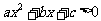的解集．

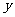(3)写出随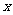的增大而减小的自变量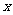的取值范围．

(4)若方程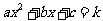有两个不相等的实数根，求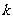的取值范围．

25．(8分) 某校的围墙上端由一段段相同的凹曲拱形栅栏组成，如图4所示，其拱形图形为抛物线的一部分，栅栏的跨径AB间，按相同的间距0.2米用5根立柱加固，拱高OC为0.6米．

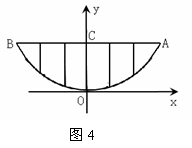(1) 以O为原点，OC所在的直线为y轴建立平面直角坐标系，请根据以上的数据，求出抛物线y=ax²的解析式；

(2)计算一段栅栏所需立柱的总长度(精确到0.1米)

24．(8分)已知抛物线C₁的解析式是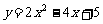，抛物线C₂与抛物线C₁关于x轴对称，求抛物线C₂的解析式．

23．(8分)如图：在四边形ABCD中，AD=BC，E、F、G分别是AB、CD、AC的中点。

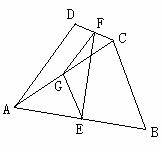求证：∠GFE=∠GEF.