
题目列表(包括答案和解析)
7、如图,在△ABC中,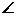 C=90°,AC=3,D为BC上一点,过点D作DE
C=90°,AC=3,D为BC上一点,过点D作DE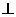 BC交AB于E,若ED=1,BD=2,则DC的长为___________
BC交AB于E,若ED=1,BD=2,则DC的长为___________
6、如图,在仝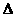 ABC中,DE//BC,若
ABC中,DE//BC,若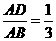 ,DE=2,则BC的长为___________。
,DE=2,则BC的长为___________。
5、如图,某建筑物BC直立于水平面,AC=9米,要建造阶梯AB,使每阶高不超过20厘米,则此阶梯最少要建___________阶。
(若最后一阶高不足20厘米时,按一阶计算,参考数据: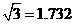 )
)
4、已知A、B是抛物线y=x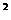 一4x+3上位置不同的两点,且关于抛物线的对称轴对称,则点A、B的坐标可能是______________________。(写出一对即可)
一4x+3上位置不同的两点,且关于抛物线的对称轴对称,则点A、B的坐标可能是______________________。(写出一对即可)
3、梯形ABCD中,腰长AB=4,底角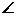 B=60°,
B=60°,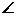 C=45°,则梯形的腰CD=___________。
C=45°,则梯形的腰CD=___________。
2、将抛物线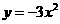 向上平移一个单位后,得到的抛物线解析式是___________。
向上平移一个单位后,得到的抛物线解析式是___________。
1、某坡面的坡度为1: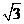 ,则坡角是___________度。
,则坡角是___________度。
25.(本题满分8分)
解:(1)如图所示,∵点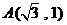 关于
关于 轴的对称点为
轴的对称点为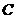 ,
, 与
与 轴交于点
轴交于点 ,
,
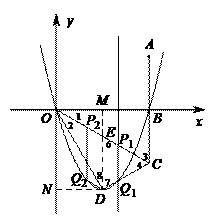 ∴
∴ ⊥
⊥ 轴于
轴于 ,
,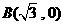 ,
,
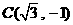 .…………………………1分
.…………………………1分
∴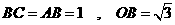 .
.
∴ ,
,
由题意可知 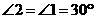 ,
, 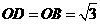 .
.
∴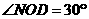 .
.
过点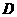 作
作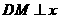 轴于
轴于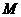 ,
,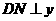 轴于
轴于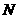 ,
,
在 中,
中,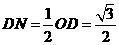 ,
, 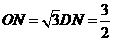 .
.
由矩形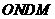 得
得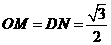 .
.
∵点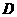 在第四象限,
在第四象限,
∴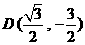 .…………………………………………2分
.…………………………………………2分
(2)设经过 、
、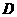 、
、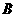 三点的抛物线的解析式为
三点的抛物线的解析式为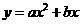 .
.
依题意得 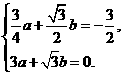 ………………………3分
………………………3分
解得 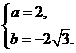
∴此抛物线的解析式为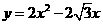 .………………………4分
.………………………4分
(3)∵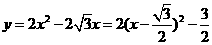 ,
,
∴点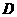 为抛物线的顶点.
为抛物线的顶点.
∴直线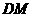 为抛物线的对称轴,交
为抛物线的对称轴,交 于
于 ,
,
由题意可知 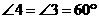 ,
,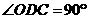 ,
,
∴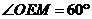 ,
,
∴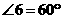 ,
,
∴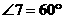 ,
,
∴ 是等边三角形,
是等边三角形,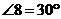 .
.
∴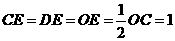 .
.
①当点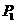 在
在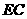 上时,四边形
上时,四边形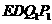 为等腰梯形.
为等腰梯形.
∵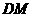 ∥
∥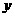 ∥
∥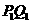 ,
,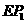 与
与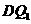 不平行,
不平行,
∴四边形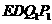 为梯形.
为梯形.
要使梯形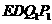 为等腰梯形,只需满足
为等腰梯形,只需满足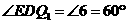 .
.
∵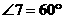 ,
,
∴点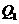 在
在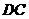 上.
上.
由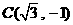 、
、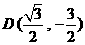 求得直线
求得直线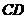 的解析式为
的解析式为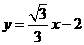 .
.
又∵点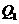 在抛物线上,∴
在抛物线上,∴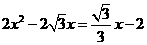 .
.
解得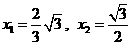 (与点
(与点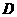 重合,舍).
重合,舍).
∴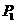 点横坐标为
点横坐标为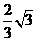 .
.
由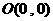 、
、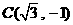 求得直线
求得直线 的解析式为
的解析式为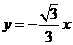 .
.
∵点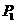 在
在 上,∴
上,∴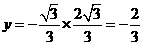 .∴
.∴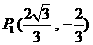 .………6分
.………6分
②当点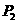 在
在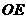 上时,四边形
上时,四边形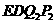 为平行四边形,此时
为平行四边形,此时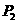 点坐标为
点坐标为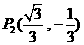 . ……………………8分
. ……………………8分
综上所述,当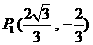 时,
时,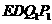 为等腰梯形;当
为等腰梯形;当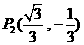 时,
时,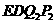 为平行四边形.
为平行四边形.
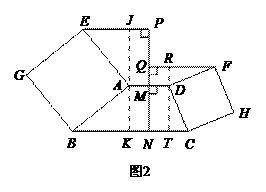
24.(本题满分7分)
证明:(1)线段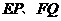 的数量关系为相等.……………………1分
的数量关系为相等.……………………1分
∵ ,
, ,
,
∴ ,
,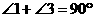 .
.
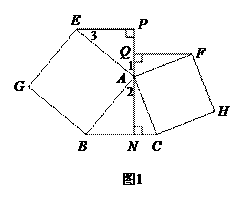 又∵四边形
又∵四边形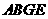 是正方形,
是正方形,
∴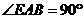 ,
,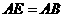 ,
,
∴ .
.
∴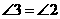 .
.
∴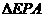 ≌
≌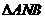 .
.
∴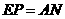 .……………………2分
.……………………2分
同理可证 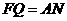 .…………3分
.…………3分
∴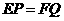 . ……………………4分
. ……………………4分
(2)过点 作
作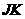 ⊥
⊥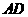 交
交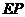 于
于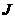 ,交
,交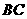 于
于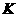 ,
,
过点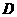 作
作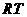 ⊥
⊥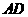 交
交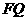 于
于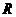 ,交
,交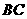 于
于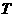 .
.
 ∵
∵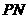 ⊥
⊥ 于
于 ,
,
∴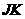 ∥
∥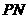 .
.
∵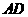 ∥
∥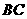 ,
,
∴四边形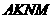 为平行四边形.
为平行四边形.
∴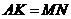 .
.
同理可得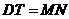 .
.
∴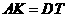 .…………………5分
.…………………5分
又∵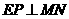 ,
,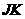 ∥
∥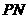 ,
,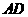 ∥
∥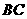 ,
,
∴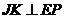 ,
,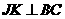 ,
,
同(1)的证明可得
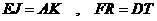 .
.
∴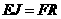 .
.
由平行四边形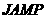 和
和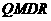 可知
可知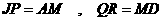 .
.
又∵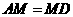 ,
,
∴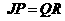 .…………………………………………6分
.…………………………………………6分
∴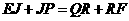 .
.
∴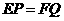 .…………………………………………7分
.…………………………………………7分
23.(本小题满分6分)
解:(1)依题意,得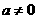 ,
,
∴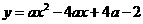
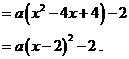
∴抛物线的顶点坐标为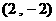 .……………………………………………2分
.……………………………………………2分
(2)∵抛物线与 轴交于整数点,
轴交于整数点,
∴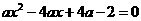 的根是整数.
的根是整数.
∴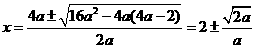 是整数.
是整数.
∵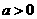 ,
,
∴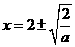 是整数.…………………………………………3分
是整数.…………………………………………3分
∴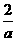 是整数的完全平方数.
是整数的完全平方数.
∵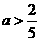 ,
,
∴ .…………………………………………4分
.…………………………………………4分
∴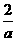 取1,4,
取1,4,
当 时,
时,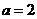 ; 当
; 当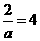 时,
时,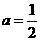 .
.
∴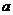 的值为2或
的值为2或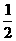 .
.
∴抛物线的解析式为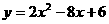 或
或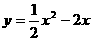 .………………6分
.………………6分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com