27、(10分)如图1，已知两个菱形ABCD和EFGH是以坐标原点O为位似中心的位似图形(菱形ABCD与菱形EFGH的位似比为2：1)，BAD=120°，对角线均在坐标轴上，抛物线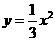经过AD的中点M．

　(1)填空：A点坐标为____________，D点坐标为____________；

(2)操作：如图2，固定菱形ABCD，将菱形EFGH绕D点顺时针方向旋转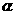度角(0°< 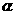<90°)，并延长OE交AD于点P，延长OH交CD于点Q．

探究1：在旋转的过程中是否存在某一角度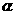，使得四边形AFEP是平行四边形?若存在，请推断出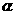的值；若不存在，说明理由；

探究2：设AP=x，四边形OPDQ的面积为S，求S与x之间的函数关系式，

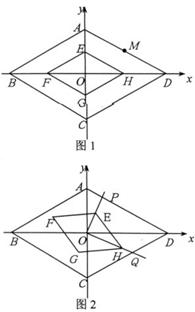并指出x的取值范围．

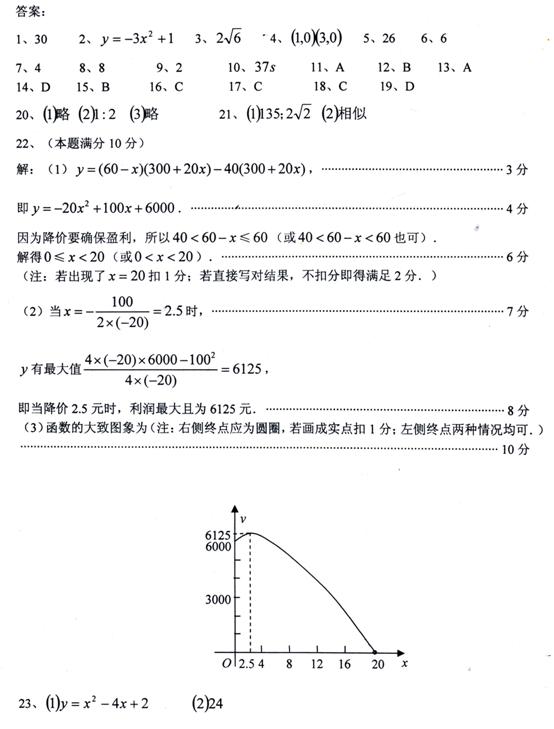
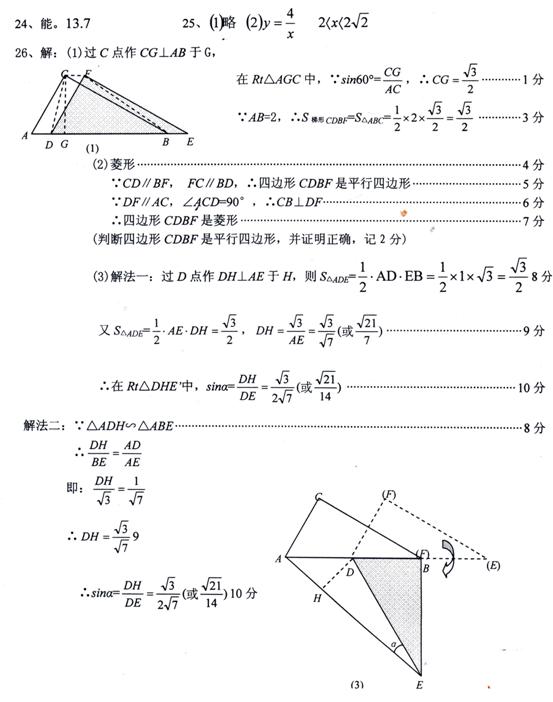
26、(10分)如图，两个全等的直角三角形ABC和DEF重叠在一起，其中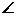A=60°，AC=1．

固定△ABC不动，将△DEF进行如下操作：

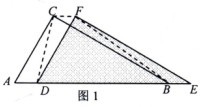
(1)如图1，△DEF沿线段AB向右平移(即点D在线段。AB内移动)，连结DC、CF、FB，四边形CDBF的形状在不断的变化，但它的面积不变化，请求出其面积．

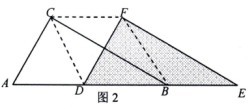
(2)如图2，当点D移到AB的中点时，请你猜想四边形CDBF的形状，并说明理由．

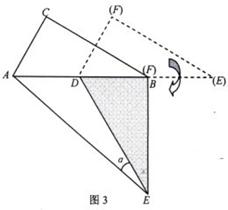
(3)如图3，△DEF的点D固定在AB的中点，然后绕点D按顺时针方向旋转△DEF，使DF落在AB边上，此时点F恰好与点B重合，连结AE，请你求出sina的值．

25、(10分)如图，正方形ABCD中，AB=2，P为BC上与B、C不重合的任意一点，DQ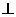AP

于点Q，

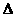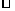
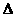(1)求证：DAQAPB；

(2)当点P在BC上运动时，线段DQ也随之变化。设PA=x，DQ=y，求y与x之间的函数

关系式，并写出x的取值范围。

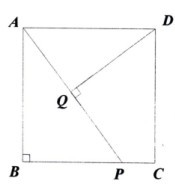
24、(10分)九(9)班的数学课外小组，对公园人工湖中的湖心亭A处到笔直的南岸的距离进

行测量．他们采取了以下方案：如图，站在湖心亭的A处测得南岸的一尊石雕C在其东南方向，再向正北方向前进10米到达B处，又测得石雕C在其南偏东30°方向．你认为此方案能够测得该公园的湖心亭A处到南岸的距离吗?若可以，请计算此距离是多少米(结果保留到小数点后一位)?

23、(10分)如图，已知抛物线y=x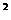+bx+c经过矩形ABCD的两个顶点A、B，AB平行于x 轴，对角线BD与抛物线交于点P，点A的坐标为(0，2)，AB=4．

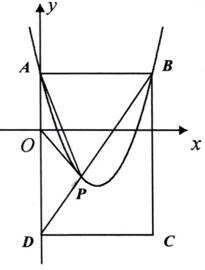(1)求抛物线的解析式；

(2)若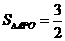，求矩形ABCD的面积．

22、(10分)某商品的进价为每件40元．当售价为每件60元时，每星期可卖出300件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出20件．在确保盈利的前提下，解答下列问题：

(1)　 若设每件降价x元、每星期售出商品的利润为y元，请写出y与x的函数关系式，并求出自变量x的取值范围；

(2)　 当降价多少元时，每星期的利润最大?最大利润是多少?

(3)　 请画出上述函数的大致图象．

21、(7分)如图，在4×4的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上。

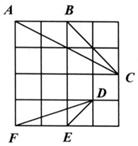(1)填空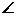：ABC=______________°，BC=____________；

(2)判断△ABC与△DEF是否相似，并证明你的结论。

20、(6分)如图，图中的小方格都是边长

为1的正方形，△ABC与△A’B’C’

是关于点O为位似中心的位似图形，

它们的顶点都在小正方形的顶点上。

(1)画出位似中心点O；

(2)△ABC与△A’B’C’的位似比为________；

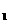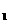(3)以点O为位似中心，再画一个△ABC，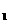

使它与△ABC的位似比等于。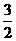

19、在△ABC中，C=90°，D是边B上一点(不与点A，B重合)，过点D作直线与另一边相交，使所得的三角形与原三角形相似，这样的直线有………………………(　　 )

A、1条　 　　　　B、2条　 　　　　C、3条 　　　　　D、4条

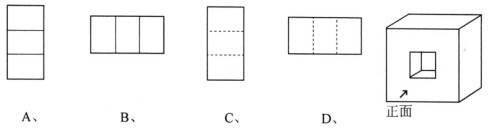
18、如图所示几何体的左视图是…………………………………………………………(　　 )