1. |-5|的相反数是(　　 )

　　　 A. 5　　　　　　　　　　　 B. -5　　　　　　　　　　 C. 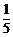　　　　　　　　　　　　　 D.

24、(本题12分)

如图，在平面直角坐标系xoy中，矩形ABCD的边AB在x轴上，

且AB=3，BC=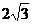，直线y=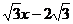经过点C，交y轴于点G。

(1)点C、D的坐标分别是C(　　　　 )，D(　　　　 )；

(2)求顶点在直线y=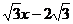上且经过点C、D的抛物线的解析式；

(3)将(2)中的抛物线沿直线y=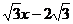平移，平移后的抛物线

交y轴于点F，顶点为点E。平移后是否存在这样的抛物线，使⊿EFG为等腰三角形？若存在，请求出此时抛物线的解析式；若不存在，请说明理由。

23、(本题10分)

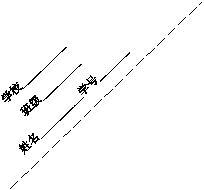
如图1，点A、B分别是两条平行线m、n上任意两点，在直线n上找一点C，使BC = kAB(k为常数)，连结AC，在直线AC上任取一点E，作∠BEF =∠ABC，EF交直线m于点F．

(1)请说明∠AFE=∠ABE的理由。

(2)当k = 1时，探究线段EF与EB的数量关系，并加以说明；

(3)当k≠1时，探究线段EF与EB的比值，请说明理由．

22、(本题10)

某工厂计划为某山区学校生产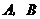两种型号的学生桌椅500套，以解决1250名学生的学习问题，一套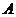型桌椅(一桌两椅)需木料，一套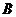型桌椅(一桌三椅)需木料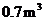，工厂现有库存木料．

(1)有多少种生产方案？

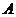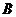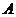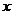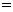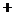(2)现要把生产的全部桌椅运往该学校，已知每套型桌椅的生产成本为100元，运费2元；每套型桌椅的生产成本为120元，运费4元，求总费用(元)与生产型桌椅(套)之间的关系式，并确定总费用最少的方案和最少的总费用．(总费用生产成本运费)

(3)按(2)的方案计算，有没有剩余木料？如果有，请直接写出用剩余木料再生产以上两种型号的桌椅，最多还可以为多少名学生提供桌椅；如果没有，请说明理由．

21、(本题8分)

保护地球，人人有则。为妥善应对气候变化, 中国作为负责任的发展中国家，主张通过切实有效的国际合作，共同应对气候变化。中学生作为全社会的一员，要加快形成低碳绿色的生活方式和消费模式，为应对气候变化做出自己的努力。在今年世界气候大会上，中国国家总理温家宝郑重向全世界公布了中国的碳减排目标，到2020年，我国单位国内生产总值二氧化碳排放比2005年下降40%－45%。风能是一种清洁能源，近几年我国风电装机容量迅速增长。下图是2003年---2009年中国风力发电装机容量统计图(单位：万千瓦)，观察统计图解答下列问题。

2003年---2009年中国风力发电装机容量统计图(单位：万千瓦)

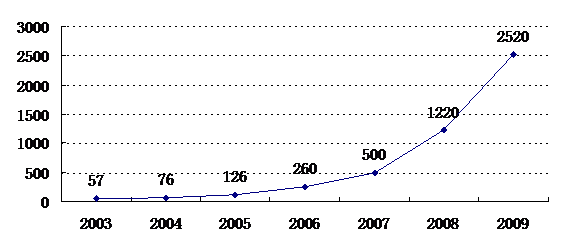
(1) 2007年，我国风力发电装机容量已达　　　　 　；

(2)从2003年到2009年，我国风力发电装机容量平均每年增长　　　 万千瓦；

(3)设2007年到2010年我国风力发电装机容量年平均增长率相同，求2010年我国风力发电装机容量。(结果精确到1万千瓦，参考数据：)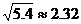

19、(本题6分)

小明手中有4张背面相同的扑克牌：红桃A、红桃2、黑桃A、黑桃2。先将4张牌背面朝上洗匀，再让小刚抽牌。

(1)小刚从中任意抽取一张扑克牌，抽到红桃的概率为　　　　　 。

(2)小刚从中任意抽取两张扑克牌。游戏规则规定：小刚抽到的两张牌是一红、一黑，则小刚胜，否则小明胜，问该游戏对双方是否公平。(利用树状图或列表说明)

　20、(本题8分)　　　　　　　　　　

如图，在网格中建立直角坐标系，Rt△ABC的顶

点A、B、C都是网格的格点(即为小正方形顶点)

(1)在网格中分别画出将△ABC向右平移2格的

△A′B′C′，和再将△A′B′C′ 绕原点O按顺时针

方向旋转90º后的△A′′B′′C′′。

(2)设小正方形边长为1，求A在两次变换中所

经过的路径总长。

18、(本题6分)

如图，已知：在 　ABCD中，E、F分别是BC、AD的中点。

(1)求证：△ABE≌△CDF　　　　　　

(2)连AC，当四边形AECF是菱形时，△ABC应满足条件　　　　　 (只需填一个条件即可)

17、(本题6分)　

计算：2sin60º--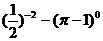

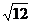
16、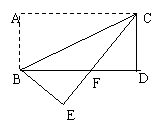如图，矩形ABCD中，AB＝12cm，BC＝18cm，直线PQ从AB出发，以1cm/s的速度向CD匀速平移，与AD，BC分别交于P，Q两点；点M从点C出发，以3cm/s的速度沿C→D→A→B→C方向逆时针运动，点M与直线PQ同时出发，当点M与点Q相遇时，点M与直线PQ都停止运动. 设△PQM的面积为S(cm²)，那么当t＝　 ▲　 s时，S＝60cm².

15、将一张长9cm 宽3cm的矩形纸片沿对角线折叠，则重叠部分的面积为　　　　　　 。

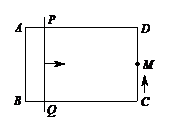
　　 (第14题)　　　　　　 (第15题)　　　　　　　　　 　　　(第16题)