4、在一个不透明的口袋中，有大小、形状完全相同，颜色不同的球15个，从中摸出红球

　 　的概率为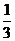，则每中红球的个数为(　　 )

A、10　　　　　　　 B、15　　　　　 C、5　　　　　 D、3

3、挺统汁，2008“超级男生”短信投票的总票数约327000000张，写成科学数法是(　　 )。

A、3．27×10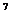　 　　B、32．7×10　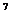　 　C．3．27×10　 　　D、3．27×10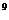

项中，只有一项是符合题目要求的)

l、下图中所示的几何体的主视图是(　 　)。

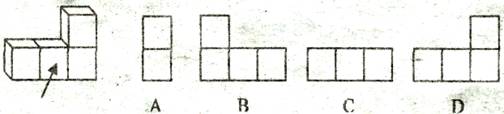
2、下列事件是必然事件的是(　　 )。

　　 A、今年10月l日湛江的天气一定是晴

　　 B、2008年奥运会刘翔一定能夺得110米跨栏冠军

　　 C、当室外遍度低于一10℃，将一豌清水放在室外会结冰

D、打开电视，正在播广告 　

­2.提示:

A(-2,0),B(0,-3),C(3,-3),D(4,0),E(3,3),F(0,3),A′(2,0),

B′(0, 3),C′(-3,-3),D′(-4,0),E′(-3,3),F′(0,3).

­3.(1)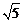,　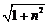 (2)解:由BE=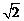,BC=1,BD=2,

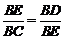∴, 且∠EBD=135°,

∴△BCE∽△BED.　

(3)解:由(2)知,△BCE∽BED,有∠BEC=∠BED,∠BCE=∠BED,

又∠BEC+∠BCE=45°,∴∠BEC+∠BED=45°,

所以②成立.

∵

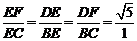
∴△BEC∽△DEF,∴∠BCE=∠DFE,

又∠BEC+ ∠BCE=45°,∴∠BEC+∠DFE=45°,所以③成立.

­4.(1)略　 (2)直角梯形.　 (3)(3000+1800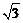)平方米.

­5.提示:(1)先得出△BCD∽△CED,∴CD²=BD.DE,

又∵AB=CD,AC=BD,∴AB²=AC·DE.　

(2)∵等腰梯形ABCD,∴OB=OC,

又Rt△BCE,∴OC=OE,∴BO=OE,

又∵AC∥EF, ∴AB=AF,∴点A是BF的中点.

­6.略

­7.解:过E作EM⊥CD于M,设EF=x,则DM=12-x.

由题意知: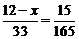,∴x=9.

又33 米高的楼是11层,

∴1层楼为3米高,因此EF是3层楼高.

∴从第4 层开始没有被前面的办公楼挡住阳光.毛

7.如图所示,有一条路CF为15米宽,这条路的北侧有一栋11层高的楼AB, 为33米的高层住宅,这条路的南侧有一栋电力公司办公楼CD,为12米高, 已知高层住宅的每层楼都一样高,当某一时刻,高层住宅楼的影长是165米,办公楼的影子映在住宅楼上,使下面的几层没有见到阳光,请你通过计算说明此刻高层住宅从第几层开始没有被前面的办公楼档住阳光.

­答案:

6.在直角坐标系内描出下列各组点,并将各组内的点用线段依次连结起来.

­　 (1)(2,0),(4,0),(2,2),(2,0);

­　 (2)(0,2),(0,4),(-2,2),(0,2);

­　 (3)(-4,0),(-2,-2),(-2,0),(-4,0);

­　 (4)(0,-2),(2,-2),(0,-4),(0,-2).

­　 观察所得的图形,你觉得它像什么?

­

5.如图所示,等腰梯形ABCD中,AD∥BC,CD⊥BD,CE⊥BC交BD的延长线于E,FE⊥AB交BA的延长线于F.

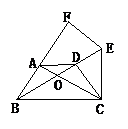­(1)试说明AB²=AC.DE；　　　　　　　 (2)试说明点A是BF的中点.

­

4.测量员在测量一块地时,站在A点(以A的正北方向为y轴的正方向,正东方向为x轴的正方向,建立坐标系),测得B(50,50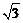),C(0,120),D(-30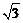,30)(单位:米),连结AB,BC,CD,DA.

­(1)画出图形; (2)这块地是什么形状? (3)求出这块地的面积.

­

3.已知:正方形的边长为1.

­(1)如图(1)所示,可以算出一个正方形的对角线长为 , 那么两个正方形并排拼成的矩形的对角线的长呢?n个正方形并排拼成的矩形的对角线长呢?

­(2)根据图(2),说明△BCE∽△BED;

­(3)由图(3),在下列所给的3个结论中, 通过合理推理选出一个正确的结论加以说明.

­　　 ①∠BEC+∠BDE=45°；　 　②∠BEC+∠BED=45°；　 　③∠BEC+∠DFE=45°.

­

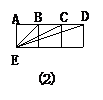
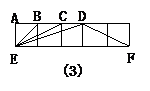
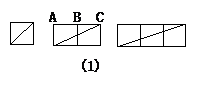
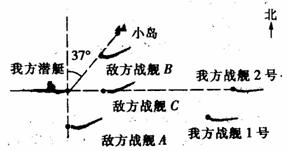­1.如图所示的是某次海军作战中敌我双方军舰对峙示意图, 请你建立适当的直角坐标系,用坐标表示出敌我军舰所在的大致位置.

­

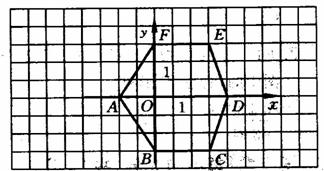
2.如图所示,写出多边形ABCDEF各个顶点的坐标,并画出多边形ABCDEF 关于y轴的轴对称图形,它们相应的对称点的坐标有什么变化?

­