28.等腰Rt△ABC和⊙O如图放置，已知AB=BC=1,∠ABC=90⁰, ⊙O的半径为1，圆心O与直线AB的距离为5.

(1)若△ABC以每秒2个单位的速度向右移动，⊙O不动，则经过多少时间△ABC的边与圆第一次相切？

(2)若两个图形同时向右移动，△ABC的速度为每秒2个单位，⊙O的速度为每秒1个单位，则经过多少时间△ABC的边与圆第一次相切？

(3)若两个图形同时向右移动，△ABC的速度为每秒2个单位，⊙O的速度为每秒1个单位，同时△ABC的边长AB、BC都以每秒0.5个单位沿BA、BC方向增大.△ABC的边与圆第一次相切时，点B运动了多少距离？

27.如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．[

容易证得：CE＝CF；[

(1) 在图1中，若G在AD上，且∠GCE＝45°，试猜想GE、BE、GD三线段之间的关系，并证明你的结论.[

(2) 在(1)的条件下,若以C为圆心，CD为半径作圆，试判断此圆与直线EG的位置关系,并说明理由.

(3) 运用⑴中解答所积累的经验和知识，完成下题：

如图2，在直角梯形ABCD中，AD∥BC(BC＞AD)，∠B＝90°，AB＝BC＝12，E是AB上一点，且∠DCE＝45°，BE＝4，求DE的长．

26. 如图，已知二次函数y=ax²-2ax+3(a<0)的图像与x轴的负半轴交于点A，与y轴的正半轴交于点B，顶点为P，且OB=3OA，一次函数y=kx+b的图像经过点A、点B．

(1)求一次函数的解析式；

(2)求顶点P的坐标；

(3)平移直线AB使其过点P，如果点M在平移后的直线上， 且tan∠OAM=，求点M的坐标．

25. 如图，甲同学正在操场上放风筝，风筝从A处起飞，几分钟后便飞达C处，此时，在AQ延长线上B处的乙同学，发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.

(1)已知旗杆高为10米，若在B处测得旗杆顶点P的仰角为30°，A处测得点P的仰角为45°，试求A、B之间的距离；

(2)此时，在A处背向旗杆又测得风筝的仰角为75°，若绳子在空中视为一条线段，求绳子AC约为多少？ (结果保留根号)

24. 如图，AB为⊙O的直径，点C在⊙O上，过点C作⊙O的切线交AB的延长线于点D，已知∠D＝30°.

(1)求∠A的度数；

(2)若点F在⊙O上，CF⊥AB，垂足为E，CF＝，求图中阴影部分的面积.[

23.如图，已知点P在x轴上，⊙P与x轴相交于A、B两点，与y轴相交于点C,若B点坐标为(1，0)，点C坐标为(0，-2)，

(1)求经过A、B、C三点的抛物线解析式；

(2)在所给的坐标系中画出抛物线的草图；

(3)观察图像，当x满足条件　　　　　 时，y<0.

22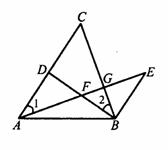．如图，D是AC上一点，BE∥AC，BE=AD，AE分别交BD、BC于点F、G，∠1=∠2.

(1)图中哪个三角形与△FAD全等？证明你的结论；

(2)探索线段BF、FG、EF之间的关系，并说明理由.

21. 有四张卡片(形状、大小和质地都相同)，正面分别写有字母A、B、C、D和一个算式．将

这四张卡片背面向上洗匀，从中随机抽取一张(不放回)，接着再随机抽取一张．

(1)用画树状图或列表法表示抽取两张卡片可能出现的所有情况(卡片可用A、B、C、D表示)；

(2)分别求抽取的两张卡片上的算式都正确的概率和只有一个算式正确的概率．

20. 先化简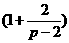÷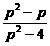，再求值(其中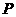是满足-3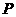＜＜3的整数)．

19．计算：