2．在下列四个图案中，既是轴对称图形，又是中心对称图形的是(　　 )

1．下列各式属于最简二次根式的是(　　 )。

　 A、　　　　　 B、　　　　 C、　　　　 D、

28. (本小题满分12分)

　 　　　如(图1)，在平面直角坐标系中，已知点，点在正半轴上，且．动点在线段上从点向点以每秒个单位的速度运动，点M、N在x轴上(M在点N的左侧)，以P、M、N为顶点的三角形是等边三角形，设运动时间为秒．

(1) 求直线的解析式；

(2) 求等边的边长(用的代数式表示)，并求出当等边的顶点运动到与原点重合时的值；

(3) 如果取的中点，以为边在内部作如图2所示的矩形，点 在线段上．设等边和矩形重叠部分的面积为，请求出当秒时与的函数关系式，并求出的最大值．

27. (本小题满分12分)

二次函数的图象的一部分如图所示．已知它的顶点M在第二象限，且经过点A(1，0)和点B(0，l)，二次函数的图象与x轴的另一个交点为C.

　 (1)试求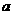，所满足的关系式；

　 (2)当△AMC的面积为△ABC面积的倍时，求a的值；

　 (3)是否存在实数a，使得△ABC为直角三角形．若存在，请求出a的值；若不存在，请说明理由．

26. (本小题满分10分)

如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC边于点D,E是边BC的中点,连接DE.

(1)求证:直线DE是⊙O的切线;

(2)连接OC交DE于点F,若OF=CF,求tan∠ACO的值.

25. (本小题满分10分)

　　 　　早晨小欣与妈妈同时从家里出发，步行与自行车向相反方向的两地上学与上班，如图是她们离家的路程(米)与时间(分钟)之间的函数图象，妈妈骑车走了10分钟时接到小欣的电话，立即以原速度返回前往学校，若已知小欣步行的速度为50米/分钟，并且妈妈与小欣同时到达学校，完成下列问题：

　　 ⑴在坐标轴两处的括号内填入适当的数据；

⑵求小欣早晨上学需要的时间。

24. (本小题满分10分)

在一个不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色外其余都相同)，其中红球有 个，蓝球有个，现从中任意摸出一个是红球的概率为．

(1)求袋中黄球的个数；

(2)第一次摸出一个球(不放回)，第二次再摸一个小球，请用画树状图或列表法求两次摸到都是红球的概率；

(3)若规定摸到红球得分，摸到黄球得分，摸到蓝球得分，小明共摸次小球(每次摸1个球，摸后放回)得分，问小明有哪几种摸法？(不分颜色的先后顺序)

23. (本小题满分8分)

如图,A、B两城市相距100km，现计划在这两座城市间修筑一条高速公路(即线段AB)，经测量，森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上.已知森林保护区的范围在以P点为圆心,50km为半径的圆形区域内.请问计划修筑的这条高速公路会不会穿越保护区?为什么?

(参考数据:)

22. (本小题满分8分)

受世界金融危机的影响，为促进内需，保持经济稳定增长，某市有关部门针对该市发放消费券的可行性进行调研.在该市16-65岁之间的居民中，进行了400个随机访问抽样调查，并根据每个年龄段的抽查人数和该年龄段对此举措的支持人数绘制了下面的统计图．

根据上图提供的信息回答下列问题：

(1)被调查的居民中，人数最多的年龄段是　　　　　 岁．

(2)已知被调查的400人中有83%的人对此举措表示支持，请你求出31-40岁年龄段的满意人数，并补全图．

(3)比较21-30岁和41-50岁这两个年龄段对此举措的支持率的高低(四舍五入到，注：某年龄段的支持率)．

21. (本小题满分8分)

如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点

叫做格点．的三个顶点、、都在格点上．

(1)画出绕点逆时针旋转后得到的三角形；

(2)求AO在上述旋转过程中所扫过的面积．