
题目列表(包括答案和解析)
3.在下列四个图案中,既是轴对称图形,又是中心对称图形的是( )

A B C D
2. 如图是一个物体的三视图,则该物体的形状是( )
如图是一个物体的三视图,则该物体的形状是( )
A.圆锥 B.圆柱
|
1.下列运算正确的是( )
A.a2·a3=a6 B.(-a2)3=-a6 C. (ab)2=ab2 D. a6÷a3=a2
26.解:(1)∵ ∴
∴
又∵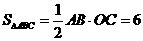 ∴
∴
∵ 为
为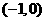 ∴
∴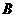 为
为
设抛物线解析式 将
将 代入求得
代入求得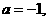
∴
(2)抛物线的对称轴为直线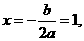 由
由
得直线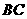 解析式为
解析式为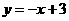
∵对称轴 与直线
与直线 相交于点
相交于点 ∴
∴ 为
为
|
 设
设 为
为 ,当
,当 时,∴
时,∴
 时, ∴
时, ∴
所以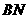 的长为3或
的长为3或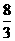
(3)存在. 由 得,抛物线的对称轴为直线
得,抛物线的对称轴为直线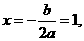 顶点
顶点 为
为
①当 时,设
时,设 点坐标为
点坐标为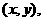 根据勾股定理,
根据勾股定理,
得 即
即
又 点
点 在抛物线上,
在抛物线上,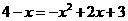 ,即
,即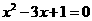 ,解得
,解得
∴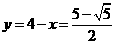 或
或 即点
即点 坐标为
坐标为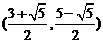 或
或 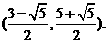
②当 时,即
时,即 关于对称轴对称
关于对称轴对称
此时 的纵坐标为3,即
的纵坐标为3,即 ,解得
,解得 (舍去),∴
(舍去),∴ 为
为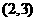
③当 时,
时, 只能在
只能在 点左边的抛物线上,所以不考虑
点左边的抛物线上,所以不考虑
∴符合条件的点 坐标为
坐标为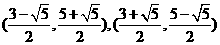 或
或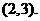
25.解:(1)设正方形的边长为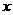 cm,则
cm,则
即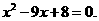 解得
解得 (不合题意,舍去),
(不合题意,舍去),
∴剪去的正方形的边长为1cm.
(2)有侧面积最大的情况.
设正方形的边长为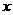 cm,盒子的侧面积为
cm,盒子的侧面积为

则 与
与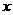 的函数关系式为:
的函数关系式为:
即 即
即
∴当 时,
时,
即当剪去的正方形的边长为2.25cm时,长方体盒子的侧面积最大为40.5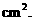
(3)设正方形的边长为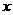 cm,盒子的侧面积为
cm,盒子的侧面积为
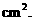
 若按图1所示的方法剪折,则
若按图1所示的方法剪折,则 与
与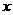 的函数关系式为:
的函数关系式为:
 即
即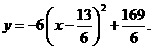
∴当 时,
时,
 若按图2所示的方法剪折,则
若按图2所示的方法剪折,则 与
与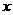 的函数关系式为:
的函数关系式为:
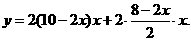 即
即
∴当 时,
时,

∵
∴当剪去正方形的边长为 cm时,盒子的侧面积最大为
cm时,盒子的侧面积最大为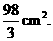
24.(1)证明:在正方形 中,
中,
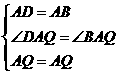 ∴
∴
 (2)解:∵
(2)解:∵ 的面积与正方形
的面积与正方形 面积之比为1:6且正方形面积为36
面积之比为1:6且正方形面积为36
∴ 的面积为6
的面积为6
过点 作
作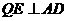 于
于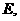
 于
于
∵ ∴
∴
∴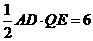 ∴
∴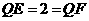
∵
∴四边形 为矩形
为矩形
∴ ∴
∴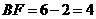
在 中,
中,
此时 在
在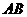 的中点位置(或者回答此时
的中点位置(或者回答此时 )
)
23.解:(1)由题得:
解得: …………2分
…………2分
(2)最喜欢足球运动的学生人数为200×15%=30(人). …………2分
(3)









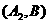

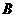


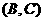



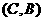
…………4分
一共有12种等可能情况,其中2人均是最喜欢篮球运动的有2种 …………1分
则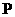 (2人都最喜欢篮球运动的学生)
(2人都最喜欢篮球运动的学生) …………1分
…………1分
 …………1分
…………1分
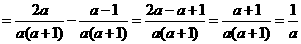 …………3分
…………3分
当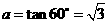 时,原式
时,原式 …………3分
…………3分
22.解:(1)把 代入
代入 得:
得: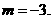
∴反比例函数的解析式为 …………2分
…………2分
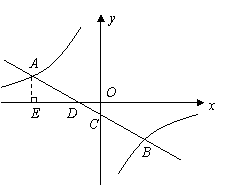 把
把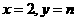 代入
代入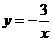 得
得 …………1分
…………1分
把
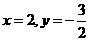 分别代入
分别代入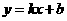
得 解得
解得
∴一次函数的解析式为 …………2分
…………2分
(2)由一次函数的解析式为 得
得 点的坐标为
点的坐标为 ∴
∴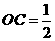
 …………3分
…………3分
(3)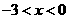 或
或 …………2分
…………2分
20.解:作 于
于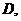 由题意知: …………1分
由题意知: …………1分

∴ ∴
∴ …………1分
…………1分
∴在 中,
中, …………1分
…………1分
在 中,
中, 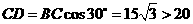 …………2分
…………2分
答:这条公路不经过该区域. …………1分
19.已知:线段 和线段
和线段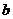 …………1分
…………1分

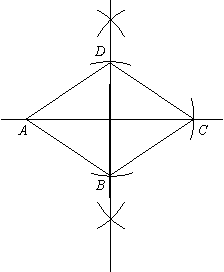 求作:菱形
求作:菱形 使
使 …………1分
…………1分
…………3分

结论:如图菱形 即为求作的图形. …………1分
即为求作的图形. …………1分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com