21、(1)50、40、30，图略；………………………….(数与图对应，每组1’，1’×3＝3’)

(2)5:4:3；……………………………………………………………………………………(1’)

(3)30；………………………………………………………………………………………(2’)

(4) 不能。…………………………………………………………………………………….(2’)

20、(1)连结O₁A、O₁B、O₂A、O₂B．……………………………………………………(1’)

证一：∵O₁是圆心，∴AO₁=BO₁，∴O₁在AB的垂直平分线上。…………………….. (2’)

同理，O₂也在AB的垂直平分线上。……………………………………………………….(1’)

∴直线O₁O₂是AB的垂直平分线。∴O₁O₂垂直平分线段AB。…………………………(2’)

证二：延长O₁O₂交AB于C。∵点O₁、O₂是圆心，∴AO₁=BO₁、AO₂=BO₂…………..(1’)

O₁O₂公用，∴△AO₁O₂≌△BO₁O₂………………………………...………………….…..…(1’)

∴∠AO₁C=∠BO₁C……………………………………………………………………………(1’)

∵AO₁=BO₁，∴△AO₁B是等腰三角形。………………………………………………..…(1’)

∴O₁O₂垂直平分线段AB。………………………………………………………………..…(1’)

(2)成立。……………………………………………………………………………………….(2’)

19、解一：x₁+x₂=3　 ………………………………………………………………………..(2’)

x₁·x₂=1， 　x₁·x₂=2……………………………………..……..…………………...(2’)

斜边长=………………….(4’)

解二：x₁·x₂=1 ，x₁·x₂=2　 ∴ m=2 …………………………………………….(2’)

x²-3x+2=0　 (x-1)(x-2)=0　 x₁=1　 x₂=2 ………………………………………………..(4’)

斜边长=………………………………………………………………..(2’)

15、C；16、B；17、D；18、D。

8、-2或x=-2； 9、1； 10、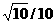； 11、10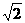； 12、2； 13、∠DPC=90⁰或∠APD=∠BCP或∠APD+∠BPC=90⁰或AP=1或AP=4等； 14、“方”或“四边”。　

1、-2； 2、x<-2/3； 3、3/x或3x^-1； 4、(x-y)(x+y+1)； 5、x>1； 6、y=2/x； 7、y²-y+2=0；

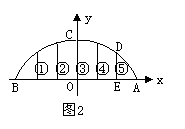
25、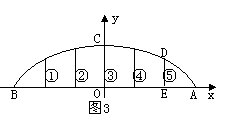如图1，抛物线关于y轴对称，顶点C坐标为(0，h )(h>0)， 交x轴于点A(d,0)、B(-d,0)(d>0)。

(1)求抛物线解析式(用h、d表示)；

(2)如图2，将ABC视为抛物线形拱桥，①-⑤拉杆均垂直x轴，垂足依次在线段AB的6等分点上。h=9米。

(i )求拉杆⑤DE的长度；

(ii)若d值增大，其他都不变，如图3。拉杆⑤DE的长度会改变吗？(只需写结论)

(3)如图4，点G在线段OA上，OG=kd(比例系数k是常数，0≤k≤1)，GF⊥x轴交抛物线于点F。试探索k为何值时，

tg∠FOG= tg∠CAO？此时点G与OA线段有什么关系？

长宁区中考数学模拟测试题答案和评分标准　　

24、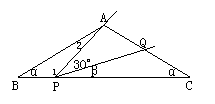如图△ABC中，∠B=∠C=α(0<α<60⁰)。将一把三角尺中30⁰角顶点P放在BC边上，当P在BC边上移动时，三角尺中30⁰角的一条边始终过点A，另一条边交AC边于点Q，P、Q不与三角形顶点重合。设∠CPQ=β。

(1)用α、β表示∠1和∠2；

(2)①当β在许可范围内变化时，α取何值总有△ABP∽△PCQ？

②当α在许可范围内变化时，β取何值总有△ABP∽△QCP？

(3)试探索有无可能使△ABP、△QPC、△ABC两两相似？若可能，写出所有α、β的值(不写过程)；若不可能，请说明理由。

23、如图，扇形中∠AOB=45⁰，半径OB=2。矩形PQRS的顶点P、S在半径OA上，Q在半径OB上，R在 弧AB上。连结OR。

(1)当∠AOR=30⁰时，求OP长；

(2)设OP=x，OS=y，求y与x的函数关系及定义域。

22、甲、乙两城市间铁路长200千米。2004年火车再次提速后速度比2002年增加了50千米/小时，故运行时间比2002年减少了2小时。

(1)求2002年火车速度；

(2)火车在2003年也曾提速，求2003年和2004年两次提速平均每次提速的百分比。

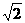(≈1.414，≈1.732)