
题目列表(包括答案和解析)
1.一9的倒数是 [ ]
(A)一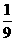 (B)
(B) 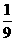 (C)一9
(D)9
(C)一9
(D)9
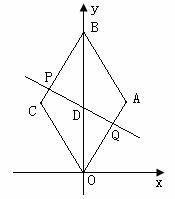
28. (本题12分)已知:如图,在平面直角坐标系中,四边形ABCO是菱形,且∠AOC=60°,点B的坐标是(0,8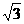 ),点P从点C开始以每秒1个单位长度的速度在线段CB上向点B移动,同时,点Q从点O开始以每秒a(1≤a≤3)个单位长度的速度沿射线OA方向移动,设t(0<t≤8)秒后,直线PQ交OB于点D.
),点P从点C开始以每秒1个单位长度的速度在线段CB上向点B移动,同时,点Q从点O开始以每秒a(1≤a≤3)个单位长度的速度沿射线OA方向移动,设t(0<t≤8)秒后,直线PQ交OB于点D.
(1)求∠AOB的度数及线段OA的长
(2)求经过A、B、C三点的抛物线的解析式;
(3)当a=3,OD=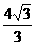 时,求t的值及此时直线PQ的解析式;
时,求t的值及此时直线PQ的解析式;
(4)当a为何值时,以O、Q、D为顶点的三角形与△OAB相似?当a为何值时,以O、Q、D为顶点的三角形与△OAB不相似?请给出你的结论,并加以说明.
27. (本题12分)几何模型:
条 件:如下左图, 、
、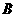 是直线
是直线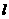 同旁的两个定点.
同旁的两个定点.
问 题:在直线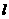 上确定一点
上确定一点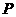 ,使
,使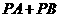 的值最小.
的值最小.
方 法:作点 关于直线
关于直线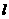 的对称点
的对称点 ,连结
,连结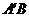 交
交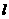 于点
于点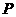 ,则
,则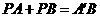 的值最小(不必证明).
的值最小(不必证明).
模型应用:
(1)如图1,正方形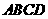 的边长为2,
的边长为2,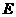 为
为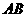 的中点,
的中点,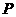 是
是 上一动点.连结
上一动点.连结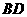 ,由正方形对称性可知,
,由正方形对称性可知,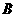 与
与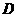 关于直线
关于直线 对称.连结PE、PB,则
对称.连结PE、PB,则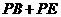 的最小值是___________;
的最小值是___________;
(2)如图2, 的半径为2,点
的半径为2,点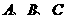 在
在 上,
上,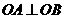 ,
,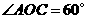 ,
,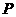 是
是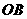 上一动点,求
上一动点,求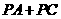 的最小值;
的最小值;
(3)如图3,∠AOB=30°,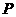 是
是 内一点,PO=8,
内一点,PO=8,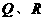 分别是
分别是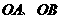 上的动点,
上的动点,
求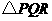 周长的最小值.
周长的最小值.
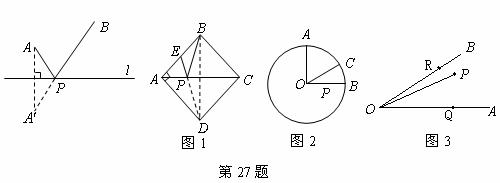
26. (本题10分) 、
、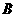 两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往
两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往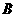 城,乙车驶往
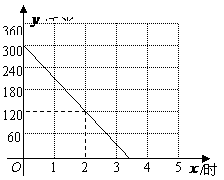
城,乙车驶往 城,甲车在行驶过程中速度始终不变.甲车距
城,甲车在行驶过程中速度始终不变.甲车距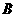 城高速公路入口处的距离
城高速公路入口处的距离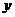 (千米)与行驶时间
(千米)与行驶时间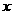 (时)之间的关系如图.
(时)之间的关系如图.
(1)求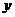 关于
关于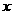 的表达式;
的表达式;
(2)已知乙车以60千米/时的速度匀速行驶,设在相遇前的行驶过程中,两车相距的路程为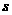 (千米).请直接写出
(千米).请直接写出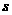 关于
关于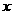 的表达式;
的表达式;
 (3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为
(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为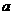 (千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度
(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度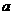 .
.
并在下图中画出乙车离开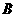 城高速公路入口处的距离
城高速公路入口处的距离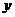 (千米)与行驶时间
(千米)与行驶时间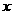 (时)之间的函数图象.
(时)之间的函数图象.
25.(本题10分)某汽车制造厂开发了一款新式电动汽车,计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人;他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发2000元的工资,给每名新工人每月发1200元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额W(元)尽可能的少?
24. (本题10分)已知:如图,O为平面直角坐标系的原点,半径为1的⊙B经过点O,且与x轴、y轴分别交于点A、C,点A的坐标为(
(本题10分)已知:如图,O为平面直角坐标系的原点,半径为1的⊙B经过点O,且与x轴、y轴分别交于点A、C,点A的坐标为(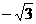 ,0),AC的延长线与⊙B的切线OD交于点D.
,0),AC的延长线与⊙B的切线OD交于点D.
(1)求OC的长度和∠CAO的度数
(2)求过D点的反比例函数的表达式.
23.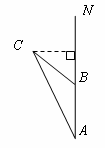 (本题10分)青海玉树地震发生后,一支专业搜救队驱车前往灾区救援.如图,汽车在一条南北走向的公路上向北行驶,当在A处时,车载GPS(全球卫星定位系统)显示村庄C在北偏西26°方向,汽车以35km/h的速度前行2h到达B处,GPS显示村庄C在北偏西52°方向.
(本题10分)青海玉树地震发生后,一支专业搜救队驱车前往灾区救援.如图,汽车在一条南北走向的公路上向北行驶,当在A处时,车载GPS(全球卫星定位系统)显示村庄C在北偏西26°方向,汽车以35km/h的速度前行2h到达B处,GPS显示村庄C在北偏西52°方向.
(1)求B处到村庄C的距离;
(2)求村庄C到该公路的距离.(结果精确到0.1km)
(参考数据: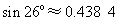 ,
,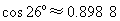 ,
,
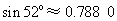 ,
,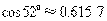 )
)
22.(本题8分)已知:如图,梯形ABCD中,AB//DC,E是BC的中点,AE、DC的延长线相交于点F,连接AC、BF.
(1)求证:AB=CF;
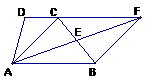 (2)若将梯形沿对角线AC折叠恰好D点与E点重合,梯形ABCD应满足什么条件,能使四边形ABFC为菱形?并加以证明.
(2)若将梯形沿对角线AC折叠恰好D点与E点重合,梯形ABCD应满足什么条件,能使四边形ABFC为菱形?并加以证明.
21.(本题8分)不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其余都相同),其中红球2个(分别标有1号、2号),蓝球1个,若从中任意摸出一个球,它是蓝球的概率为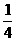 .
.
(1)求袋中黄球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用画树状图或列表格的方法,求两次摸到不同颜色球的概率.
20.(本题8分)我市各学校九年级学生在体育测试前,都在积极训练自己的考试项目,王强就本班同学“自己选测的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
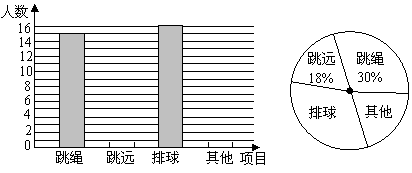
(1)该班共有 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“排球”部分所对应的圆心角度数为 °;
(4)若全校有360名学生,请计算出全校“其他”部分的学生人数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com