
题目列表(包括答案和解析)
3.下列过原点的抛物线是 ( )
A.y=2x2-1 B. y=2x2+1 C. y=2(x+1)2 D. y=2x2+x
2.抛物线y=x2-ax+a-2与坐标轴的交点个数有( )
A.3个 B.2个 C.1个 D.0个
1.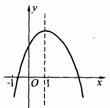 已知二次函数y=ax2+bx+c的图象如图,下列结论中,正确的结论的个数有 (
)
已知二次函数y=ax2+bx+c的图象如图,下列结论中,正确的结论的个数有 (
)
① a + b + c>0 ② a - b + c<0 ③ abc < 0 ④ b =2a ⑤ b >0
A. 5个 B. 4个 C .3个 D. 2个
25、(14分)如图,在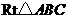 中,
中,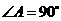 ,
,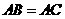 ,
,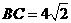 ,另有一等腰梯形
,另有一等腰梯形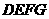 (
(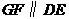 )的底边
)的底边 与
与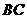 重合,两腰分别落在
重合,两腰分别落在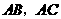 上,且
上,且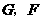 分别是
分别是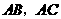 的中点.
的中点.
(1)求等腰梯形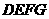 的面积;
的面积;
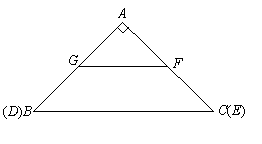
(2)操作:固定 ,将等腰梯形
,将等腰梯形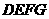 以每秒1个单位的速度沿
以每秒1个单位的速度沿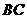 方向向右运动,直到点
方向向右运动,直到点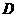 与点
与点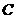 重合时停止.设运动时间为
重合时停止.设运动时间为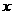 秒,运动后的等腰梯形为
秒,运动后的等腰梯形为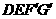 (如图).
(如图).
探究1:在运动过程中,四边形 能否是菱形?若能,请求出此时
能否是菱形?若能,请求出此时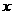 的值;若不能,请说明理由.
的值;若不能,请说明理由.
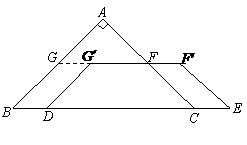
探究2:设在运动过程中 与等腰梯形
与等腰梯形 重叠部分的面积为
重叠部分的面积为 ,求
,求 与
与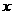 的函数关系式.
的函数关系式.
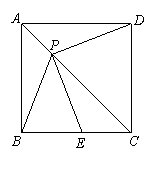
24、(12分)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.
(1)求证:① PE=PD ; ② PE⊥PD;
(2)设AP=x, △PBE的面积为y.
① 求出y关于x的函数关系式,并写出x的取值范围;
② 当x取何值时,y取得最大值,并求出这个最大值.
23、(10分)为了迎接省运会,市园林处对一段公路进行绿化,计划购买甲、乙两种风景树共600棵.甲、乙两种树的相关信息如下表:
|
项目 品种 |
单价(元/棵) |
成活率 |
|
甲 |
60 |
88% |
|
乙 |
80 |
96% |
(1)若购买树苗的总费用不超过44000元,则最多可购买乙种树苗多少棵?
(2)若希望这批树的成活率不低于90%,并使购买树苗的总费用最低,应如何选购树苗?购买树苗的最低费用为多少?
22、(10分)已知:如图,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1) 求证:DE是⊙O的切线.
(2)作DG⊥AB交⊙O于G,垂足为F, 若∠C=30°, CB =8 ,
 求弦DG的长.
求弦DG的长.
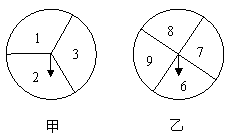
21、(8分)如图是两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字.小亮和小颖利用它们做游戏,游戏规则是:
同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于10,小颖获胜;指针所指区域内的数字之和等于10,为平局;指针所指区域内的数字之和大于10,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.
(1)请你通过画树状图的方法求小颖获胜的概率.
(2)你认为该游戏规则是否公平?若游戏规则公平,请说明理由;若游戏规则不公平,请你设计出一种公平的游戏规则.
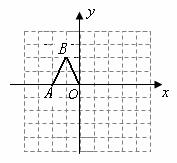
20、(8分)如图,在边长均为1的小正方形网格纸中,△ 的顶点
的顶点 、
、 、
、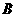 均在格点上,且
均在格点上,且 是直角坐标系的原点,点
是直角坐标系的原点,点 在轴上.
在轴上.
(1)以 为位似中心,将△
为位似中心,将△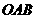 放大,使得放大后的△
放大,使得放大后的△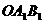 与
与
△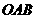 对应线段的比为2∶1,画出△
对应线段的比为2∶1,画出△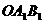 .(所画△
.(所画△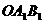 与△
与△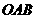 在原点两侧).
在原点两侧).
(2)求出线段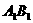 所在直线的函数关系式.
所在直线的函数关系式.
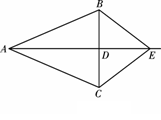
19、(8分)如图,在△ABC中,AB=AC,D是BC的中点,连结AD,在AD的延长线上取一点E,连结BE,CE.
(1)求证:△ABE≌△ACE
(2)当AE与AD满足什么数量关系时,四边形ABEC是菱形?并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com