5.一个函数的图象是一条以y轴为对称轴，以原点为顶点的抛物线，且经过点A(-2,8).

(l)求这个函数的解析式；

(2)画出函数图象；

(3)写出抛物线上与点A关于y轴对称的点B的坐标，并计算△OAB的面积．

课外拓展练习

●A组　　 基础练习

4.函数y=3x²与函数y=-3x²的图象的形状　　　 ，但　　　 不同.

●B组　　 提高训练

3.函数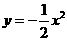的对称轴是　　　　 ，顶点坐标是　　　 ，对称轴的右侧y随x的增大而　　 ，当x=　 时，

函数y有最　　　 值，是　　　　 .

2．当a>0时，y=ax²在x轴上的　　　 (其中顶点在　　　 轴上),它的开口　　　 并且向上无限　　　 .

1．函数y=ax²(a≠0)的图象叫做　　　　　　　 ，它关于　　　 轴对称，它的顶点是　　　　 .

3.函数y=ax²,当a>0时，对称轴的左侧y随x的增大而减小，对称轴的右侧y随x的增大而增大；当x=0时函数y有最小值0.

课内同步精练

●A组　　 基础练习

2.函数y=ax²,当a>0时，抛物线的开口向上；当a<0时，抛物线开口向下.

1.函数y=ax²的图象是一条抛物线，它的对称轴是y轴，图像的顶点是(0,0)

2.2 二次函数的图象 同步练习

[知识要点]

2．函数y=x²与y=－x²的图象关于　　　　 对称，也可以认为函数y=－x²的图象，是函数y=x²的图象绕　　　　 旋转得到的．

⒊抛物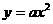线与直线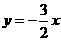交于(1，)，则其解析式为　　　　　 ，对称轴是　　　　 ，顶点坐标是　　　 ，当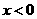时，y随x的增大而　　 ，当x=　 时，函数y有最　　　 值，是　　　　 .

⒋已知a＜－1，点(a－1，y₁)、(a，y₂)、(a+1，y₃)都在函数y= -x²的图象上，则(　　　 )

A．y₁＜y₂＜y₃ B．y₁＜y₃＜y₂ C．y₃＜y₂＜y₁ D．y₂＜y₁＜y₃

⒌如图，A、B分别为y=x²上两点，且线段AB⊥y轴，若AB=6，则直线AB的表达式为(　　　 )

A．y=3　　 B．y=6　　 C．y=9　　 D．y=36

⒍对于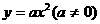的图象下列叙述正确的是　　　　　 (　　 )

A　 的值越大，开口越大　　　　　 B　　 的值越小，开口越小

C　 的绝对值越小，开口越大　　　 D　　 的绝对值越小，开口越小

⒎一个函数的图象是一条以y轴为对称轴，以原点为顶点的抛物线，且经过点A(2,-8).(l)求这个函数的解析式； (2)画出函数图象； (3)观察函数图象，写出这个函数所具有的性质。

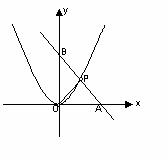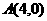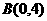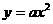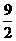⒏已知，如图，直线经过和两点，它与抛物线在第一象限内相交于点P，又知的面积为，求的值；

⒐如图，在以O为圆心的两个同心圆中，小圆的半径长为2，大圆的弦AB与小圆交于点C、D，且∠COD＝60°，CD=CA。

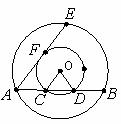(Ⅰ)求大圆半径的长；

(Ⅱ)若大圆的弦AE与小圆切于点F，求AE的长.

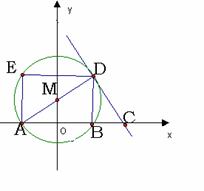
⒑如图，在直角坐标系中，点M在y轴的正半轴上，⊙M与x轴交于A,B两点，AD是⊙M的直径，过点D作⊙M的切线，交x轴于点C.已知点A的坐标为(-3，0),点C的坐标为(5,0)。⑴求点B的坐标和CD的长；⑵过点D作DE∥BA，交⊙M于点E，连结DB,AE，求AE的长。

⒒如图，在直角梯形ABCD中，AD∥BC，∠C＝90°，BC＝16，DC＝12，AD＝21。动点P从点D出发，沿射线DA的方向以每秒2两个单位长的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长的速度向点B运动，点P，Q分别从点D，C同时出发，当点Q运动到点B时，点P随之停止运动。设运动的时间为t(秒)。

(1)设△BPQ的面积为S，求S与t之间的函数关系式；

(2)当t为何值时，以B，P，Q三点为顶点的三角形是等腰三角形？

(3)当线段PQ与线段AB交于O，且2AO＝OB时，求∠BQP的正切值；

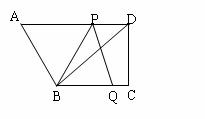(4)是否存在时刻t，使得PQ⊥BD？若存在，求出t的值；若不存在，请说明理由。