2．抛物线y =x² –2x –3　的对称轴和顶点坐标分别是(　　 )

A．x =1，(1，-4)　 B．x =1，(1，4)　 C．x=-1，(-1，4)　 D．x =-1，(-1，-4)

1．下列函数关系中，可以看做二次函数y=ax² +bx +c(a≠0)模型的是(　 )

A．在一定的距离内汽车的行驶速度与行驶时间的关系

B．我国人口年自然增长率1%，这样我国人口总数随年份的关系

C．竖直向上发射的信号弹，从发射到落回地面，信号弹的高度与时间的关系(不计空气阻力)

D．圆的周长与圆的半径之间的关系．

23．(12分)已知y=ax²+bx+c与y轴交于点A(0，3)，与x轴分别交于B(1，0)、C(5，0)两点.

(1)求此抛物线的解析式；

(2)若点D为线段OA的一个三等分点，求直线DC的解析式；

(3)若一个动点P自OA的中点M出发，先到达x轴上的某点(设为点E)，再到达抛物线的对称轴上某点(设为点F)，最后运动到点A.求使点P运动的总路径最短的点E、点F的坐标，并求出这个最短总路径的长.

22．(10分)如图，有一座抛物线形拱桥，在正常水位时水面AB的宽是20米，如果水位上升3米时，水面CD的宽为10米.

　 (1)建立如图所示的直角坐标系，求此抛物线的解析式.

(2)现有一辆载有救援物质的货车从甲地出发，要经过此桥开往乙地，已知甲地到此桥为280千米(桥长忽略不计)，货车以每小时40千米的速度开往乙地，当行驶1小时时，忽然接到紧急通知，前方连降大雨，造成水位以每小时0.25米的速度持续上涨(货车接到通知时水位在CD处)，当水位达到桥拱最高点O时，禁止车辆通行.试问：汽车按原来速度行驶，能否安全通过此桥？若能，请说明理由；若不能，要使货车安全通过此桥，速度应超过多少千米/时？

21．(10分)利达经销店为某工厂代销一种建筑材料．当每吨售价为260元时，月销售量为45吨．该经销店为提高经营利润，准备采取降价的方式进行促销．经市场调查发现：当每吨售价每下降10元时，月销售量就会增加7.　5吨．综合考虑各种因素，每售出一吨建筑材料共需支付厂家及其它费用100元．设每吨材料售价为x(元)，该经销店的月利润为y(元)．

(1)当每吨售价是240元时，计算此时的月销售量；

(2)求出y与x的函数关系式(不要求写出x的取值范围)；

(3)该经销店要获得最大月利润，售价应定为每吨多少元？

(4)小静说：“当月利润最大时，月销售额也最大．”你认为对吗？请说明理由．

20．(10分)已知抛物线y＝ax²+b x+c经过A，B，C三点，当x≥0时，其图象如图所示．

(1)求抛物线的解析式，写出抛物线的顶点坐标；

(2)画出抛物线y＝ax²+b x+c当x＜0时的图象；

(3)利用抛物线y＝ax²+b x+c，写出为何值时，y＞0．

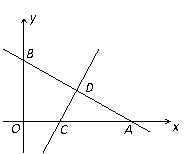
19．(8分)如图，一次函数y=kx+n的图象与x轴和y轴分别交于点A(6，0)和B(0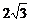，)，线段AB的垂直平分线交x轴于点C，交AB于点D.

(1)试确定这个一次函数关系式；

(2)求过A、B、C三点的抛物线的函数关系式.

18、(8分)已知二次函数y=x²-(m²+8)x+2(m²+6)，设抛物线顶点为A，与x轴交于B、C两点，问是否存在实数m,使△ABC为等腰直角三角形，如果存在求m;若不存在说明理由。

17、(8分)y= ax²+bx+c图象与x轴交于A、B与y轴交于C，OA=2，OB=1 ，OC=1，求函数解析式(求出所有可能的情况)

16.将10cm长的线段分成两部分，一部分作为正方形的一边，另一部分作为一个等腰直角三角的斜边，求这个正方形和等腰直角三角形之和的最小值为　　　　　 。