
题目列表(包括答案和解析)
4、(2007贵州贵阳课改,10分)某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格调查,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量(箱)与销售价(元/箱)之间的函数关系式.(3分)
(2)求该批发商平均每天的销售利润(元)与销售价(元/箱)之间的函数关系式.(3分)
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?(4分
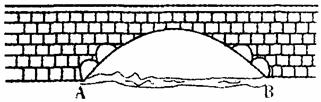
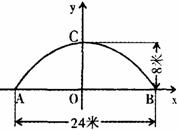
1、如图所示是永州八景之一的愚溪桥,桥身横跨愚溪,面临潇水,桥下冬暖夏凉,常有渔船停泊桥下避晒纳凉.已知主桥拱为抛物线型,在正常水位下测得主拱宽24m,最高点离水面8m,以水平线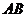 为x轴,
为x轴,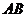 的中点为原点建立坐标系.
的中点为原点建立坐标系.
①求此桥拱线所在抛物线的解析式.
②桥边有一浮在水面部分高4m,最宽处12m的河鱼餐船,试探索此船能否开到桥下?说明理由.
2、善于不断改进学习方法的小迪发现,对解题进行回顾反思,学习效果更好.某一天小迪有20分钟时间可用于学习.假设小迪用于解题的时间(单位:分钟)与学习收益量的关系如图1所示,用于回顾反思的时间(单位:分钟)与学习收益的关系如图2所示(其中 是抛物线的一部分,为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
是抛物线的一部分,为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
(1)求小迪解题的学习收益量与用于解题的时间之间的函数关系式;
(2)求小迪回顾反思的学习收益量与用于回顾反思的时间的函数关系式;
(3)问小迪如何分配解题和回顾反思的时间,才能使这20分钟的学习收益总量最大?

2、如图,抛物线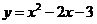 与轴分别交于,两点.
与轴分别交于,两点.
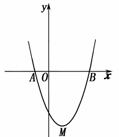 (1)求A,B两点的坐标;(2)求 抛物线顶点M关于轴对称的点
(1)求A,B两点的坐标;(2)求 抛物线顶点M关于轴对称的点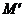 的坐标,并判断四边形AMB
的坐标,并判断四边形AMB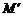 是何特殊平行四边形(不要求说明理由).
是何特殊平行四边形(不要求说明理由).
解:
1、某种爆竹点燃后,其上升的高度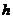 (米)和时间(秒)符合关系式
(米)和时间(秒)符合关系式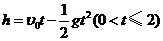 ,其中重力加速度以
,其中重力加速度以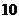 米/秒
米/秒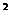 计算.这种爆竹点燃后以
计算.这种爆竹点燃后以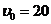 米/秒的初速度上升,
米/秒的初速度上升,
(1)这种爆竹在地面上点燃后,经过多少时间离地15米?
(2)在爆竹点燃后在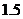 秒至
秒至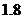 秒这段时间内,判断爆竹是上升,或是下降,并说明理由.
秒这段时间内,判断爆竹是上升,或是下降,并说明理由.
8、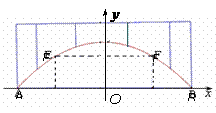 廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为
廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为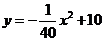 ,为保护廊桥的安全,在该 抛物线上距水面
,为保护廊桥的安全,在该 抛物线上距水面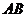 高为8米的点、处要安装两盏警示灯,则这两盏灯的水平距离
高为8米的点、处要安装两盏警示灯,则这两盏灯的水平距离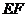 是
( 米(精确到1米).
是
( 米(精确到1米).
7、飞机着陆后滑行的距离(单位:米)与滑行的时间(单位:秒)之间的函数关系式是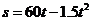 .飞机着陆后滑行 秒才能停下来.
.飞机着陆后滑行 秒才能停下来.
6、 已知二次函数
已知二次函数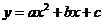 的图象如图所示,则点(a+b, c)在第
( 象限
的图象如图所示,则点(a+b, c)在第
( 象限
5、已知二次函数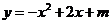 的部分图象如图所示,
的部分图象如图所示,
则关于的一 元二次方程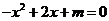 的解为
.
的解为
.
4、 当
当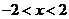 时,下列函数中,函数值随自变量增大而增大的是 (只填写序号)①
时,下列函数中,函数值随自变量增大而增大的是 (只填写序号)①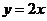 ;②
;②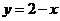 ;③
;③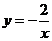 ;④
;④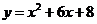
3、已知二次函数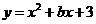 的对称轴为
的对称轴为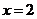 ,则
,则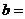 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com