
题目列表(包括答案和解析)
2、
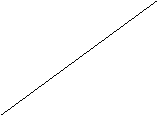


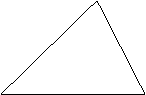 作下列三角形的外接圆:
作下列三角形的外接圆:

问题:(1)经过一个已知点可以画多少个圆?
(2)经过两个已知点可以画多少个圆?这样的圆的圆心在怎样的一条直线上?
(3)过同在一条直线上的三个点能画圆吗?
定理:经过 确定一个圆。
1、三角形的外心恰在它的一条边上,那么这个三角形是( )
A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定
4. AB为⊙0的直径,C为⊙O上一点,过C作CD⊥AB于点D,延长CD至E,使DE=CD,那么点E的位置 ( )
A.在⊙0 内 B.在⊙0上 C.在⊙0外 D.不能确定
3. ⊙0的半径为13cm,圆心O到直线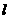 的距离d=OD=5cm.在直线
的距离d=OD=5cm.在直线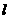 上有三点P,Q,R,且PD = 12cm , QD<12cm, RD>12cm,则点P在 ,点Q在 ,点R在
.
上有三点P,Q,R,且PD = 12cm , QD<12cm, RD>12cm,则点P在 ,点Q在 ,点R在
.
2、一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是( )
A、2.5 cm或6.5 cm B、2.5 cm C、6.5 cm D、5 cm或13cm
如果P是圆所在平面内的一点,d 表示P到圆心的距离,r表示圆的半径,则:
(1)d<r →
(2)d=r →
(3)d>r →
1、两个圆的圆心都是O,半径分别为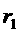 、
、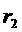 ,且
,且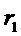 <OA<
<OA<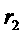 ,那么点A在( )
,那么点A在( )
A、⊙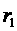 内 B、⊙
内 B、⊙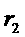 外 C、⊙
外 C、⊙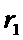 外,⊙
外,⊙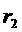 内 D、⊙
内 D、⊙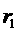 内,⊙
内,⊙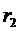 外
外
16.如图A是半圆上一个三等分点,B是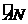 的中点,P是直径MN上一动点。已知⊙O半径为1,求AP+BP的最小值。
的中点,P是直径MN上一动点。已知⊙O半径为1,求AP+BP的最小值。
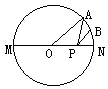
仿照上题解答以下两题:
(1)如图,在正方形ABCD中,E在BC上,且BE=2,CE=1,P在BD上,求PE+PC的最小值。
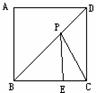
(2)如图,设正△ABC的边长为2,M是AB边的中点,P是边BC上任意一点。PA+PM的最大值和最小值分别记为s和t,求s2-t2的值。(2000年全国初中数学联赛试题)

15.如图,⊙O是ABC的外接圆,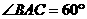 ,AD,CE分别是BC,AB上的高,且AD,CE
,AD,CE分别是BC,AB上的高,且AD,CE
交于点H,求证:AH=AO
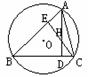
类题
(1)如图,在⊙O中,弦ACBD,OEAB,垂足为E,求证:OE=CD
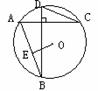
(2)如图,AC,BD是⊙O的两条弦,且ACBD,⊙O的半径为,求AB2+CD2的值。
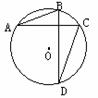
14.如图,AD是△ABC的高线,AE是△ABC的外接圆的直径,求证:∠BAE=∠DAC.

变题
(1)如图,△ABC内接于⊙O,AHBC,垂足为H,AD平分∠BAC,交⊙O于D.
求证:AD平分∠HAO.
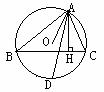
(2)已知如图△ABC内接于⊙O,ADBE于D,BEAC于E,AD,BE交于点F,延长AD交⊙O于求证:BG=BF
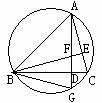
(3)如图,△ABC内接于⊙O, A的平分线与⊙O交于D,DEAB于E,DFAC于F。求证BE=CF
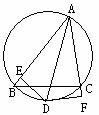
13.如图ABC是⊙O的一条折弦,BC>AB,D是ABC弧的中点,DE⊥BC,垂足为E,(1)求证:CE=BE+AB.(2)若连结DC、DB,则DC2-DB2=AB•BC.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com