
题目列表(包括答案和解析)
3、选择:(1)在Rt△ABC中,∠C=900,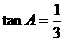 ,AC=6,则BC的长为( )
,AC=6,则BC的长为( )
A、6 B、5 C、4 D、2
(2)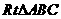 中,
中, =90,
=90,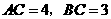 ,
,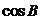 的值为 ( )
的值为 ( )
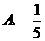
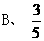
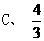
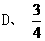
(3)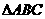 中,
中, =90,
=90,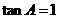 ,则
,则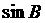 的值是 (
)
的值是 (
)
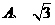
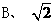
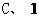
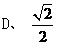
2、(1)在Rt△ABC中,∠C=900,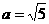 ,
,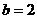 ,则sinA=
。
,则sinA=
。
(2)在Rt△ABC中,∠A=900,如果BC=10,sinB=0.6,那么AC= 。
(3)在 中,
中, =90,c = 8
, sinA =
=90,c = 8
, sinA = 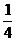 ,则
,则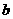 = .
= .
2、在Rt△ABC中,∠C=900,AC=12,BC=15。
(1)求AB的长; (2)求sinA、cosA的值;
(3)求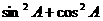 的值; (4)比较sinA、cosB的大小。
的值; (4)比较sinA、cosB的大小。
1、各三角函数之间的关系:
⑴sin=cos
; ⑵sin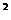 +cos
+cos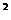 = ;
= ;
⑶tan= .
21. 解:(1)令
解:(1)令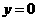 ,得
,得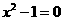 解得
解得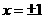
令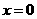 ,得
,得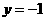
∴ A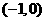 B
B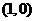 C
C ·················· (2分)
·················· (2分)
(2)∵OA=OB=OC= ∴BAC=ACO=BCO=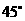
∵AP∥CB, ∴PAB=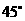
过点P作PE轴于E,则APE为等腰直角三角形
令OE=,则PE=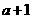 ∴P
∴P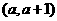
∵点P在抛物线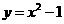 上 ∴
上 ∴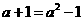
解得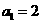 ,
,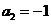 (不合题意,舍去)
(不合题意,舍去)
∴PE=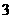 ······································································································ 4分)
······································································································ 4分)
∴四边形ACBP的面积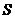 =
=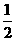 AB•OC+
AB•OC+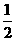 AB•PE
AB•PE
= ······················································································· 6分)
······················································································· 6分)
(3). 假设存在
∵PAB=BAC
=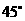 ∴PAAC
∴PAAC
∵MG轴于点G, ∴MGA=PAC
=
在Rt△AOC中,OA=OC= ∴AC=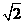
在Rt△PAE中,AE=PE=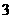 ∴AP=
∴AP= 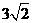 ······························································ 7分)
······························································ 7分)
设M点的横坐标为,则M 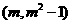
①点M在轴左侧时,则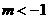
 (ⅰ) 当AMG
(ⅰ) 当AMG 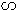 PCA时,有
PCA时,有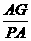 =
=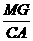
∵AG=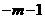 ,MG=
,MG=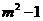
即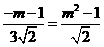
解得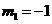 (舍去)
(舍去) 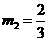 (舍去)
(舍去)
(ⅱ) 当MAG 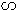 PCA时有
PCA时有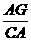 =
=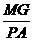
即
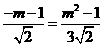
解得: (舍去)
(舍去) 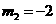
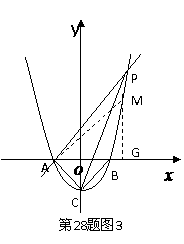 ∴M
∴M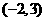 ···································································································· (10分)
···································································································· (10分)
② 点M在轴右侧时,则
(ⅰ) 当AMG 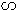 PCA时有
PCA时有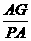 =
=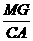
∵AG=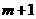 ,MG=
,MG=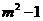
∴ 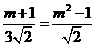
解得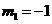 (舍去)
(舍去) 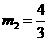
∴M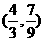
(ⅱ) 当MAG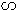 PCA时有
PCA时有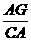 =
=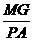
即
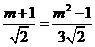
解得: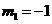 (舍去)
(舍去) 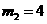
∴M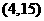
∴存在点M,使以A、M、G三点为顶点的三角形与PCA相似
M点的坐标为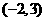 ,
,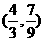 ,
,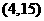 ························································· (13分)
························································· (13分)
15、解:(1)△BPQ是等边三角形,当t=2时,AP=2×1=2,BQ=2×2=4,所以BP=AB-AP=6-2=4,所以BQ=BP.又因为∠B=600,所以△BPQ是等边三角形.
(2)过Q作QE⊥AB,垂足为E,由QB=2y,得QE=2t·sin600=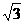 t,由AP=t,得PB=6-t,
t,由AP=t,得PB=6-t,
所以S△BPQ=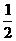 ×BP×QE=
×BP×QE=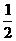 (6-t)×
(6-t)×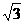 t=-
t=-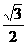 t2+3
t2+3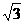 t;
t;
(3)因为QR∥BA,所以∠QRC=∠A=600,∠RQC=∠B=600,又因为∠C=600,所以△QRC是等边三角形,所以QR=RC=QC=6-2t.因为BE=BQ·cos600=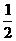 ×2t=t,所以EP=AB-AP-BE=6-t-t=6-2t,
×2t=t,所以EP=AB-AP-BE=6-t-t=6-2t,
所以EP∥QR,EP=QR,所以四边形EPRQ是平行四边形,所以PR=EQ=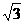 t,又因为∠PEQ=900,
t,又因为∠PEQ=900,
所以∠APR=∠PRQ=900.因为△APR-△PRQ,所以∠QPR=∠A=600,所以tan600=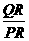 ,即
,即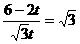 ,所以t=
,所以t=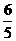 ,所以当t=
,所以当t=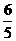 时, △APR-△PRQ
时, △APR-△PRQ
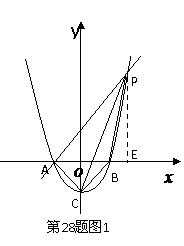
23、(2008年广东湛江市) 如图11所示,已知抛物线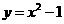 与轴交于A、B两点,与轴交于点C.
与轴交于A、B两点,与轴交于点C.
(1)求A、B、C三点的坐标.
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积.
 (3)在轴上方的抛物线上是否存在一点M,过M作MG轴于点G,使以A、M、G三点为顶点的三角形与PCA相似.若存在,请求出M点的坐标;否则,请说明理由.
(3)在轴上方的抛物线上是否存在一点M,过M作MG轴于点G,使以A、M、G三点为顶点的三角形与PCA相似.若存在,请求出M点的坐标;否则,请说明理由.
22. (10分)将一副三角板按如图的方式摆放在一起,连接AD,求∠ADB的正弦值
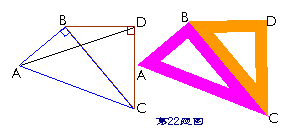
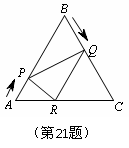
21、(2008年福建省福州市)如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR//BA交AC于点R,连结PR,当t为何值时,△APR∽△PRQ?

20.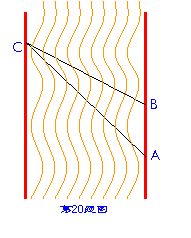 (10分)在一次数学活动课上,胡老师带领九(3)班的同学去测
(10分)在一次数学活动课上,胡老师带领九(3)班的同学去测
一条南北流向的河宽。如图所示,张一凡同学在河东岸点A出测到河
对岸边有一点C,测得C在A的北偏西31°的方向上,沿河岸向北
前进21m到达B处,测得C在B的北偏西45°的方向上。
请你根据以上的数据,帮助该同学计算出这条河的宽度。(tan31°=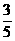 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com