
题目列表(包括答案和解析)
(1)如图4-6-8,在△ABC中,AC是BC、DC的比例中项,则△ABC∽________,理由是________.
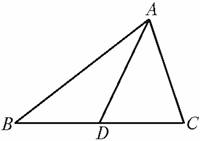
图4-6-8
(2)如图4-6-9,D、E、F分别是△ABC各边的中点,则△DEF∽________,理由是________.
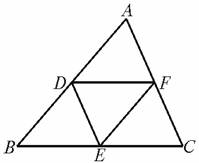
图4-6-9
(3)如图4-6-10,∠BAD=∠CAE,∠B=∠D,AB=2AD,若BC=3 cm,则DE=________cm.
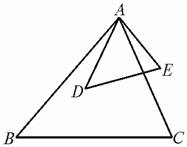
图4-6-10
(4)如图4-6-11,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端分别在CB、CD上滑动,那么当CM=________时,△ADE与△MNC相似.
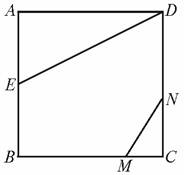
图4-6-11
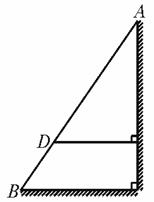
图4-6-7
如图4-6-7,长梯AB斜靠在墙壁上,梯脚B距墙80 cm,梯上点D距墙70 cm,量得BD长55 cm,求梯子的长.
(1)下列各组图形中有可能不相似的是( )
A.各有一个角是45°的两个等腰三角形
B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形
D.两个等腰直角三角形
(2)△ABC和△A′B′C′符合下列条件,其中使△ABC和△A′B′C′不相似的是( )
A.∠A=∠A′=45° ∠B=26° ∠B′=109°
B.AB=1 AC=1.5 BC=2 A′B′=4 A′C′=2 B′C′=3
C.∠A=∠B′ AB=2 AC=2.4 A′B′=3.6 B′C′=3
D.AB=3 AC=5 BC=7 A′B′=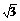 A′C′=
A′C′=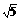 B′C′=
B′C′=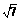
(3)如图4-6-5,AB∥CD,AD与BC相交于点O,那么在下列比例式中,正确的是( )
A.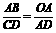 B.
B.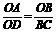
C.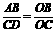 D.
D.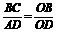
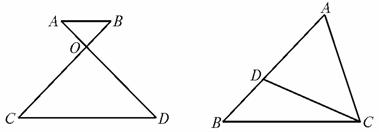
图4-6-5 图4-6-6
(4)如图4-6-6,D为△ABC的边AB上一点,且∠ABC=∠ACD,AD=3 cm,AB=4 cm,则AC的长为( )
A.2 cm B.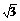 cm
cm
C.12 cm D.2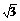 cm
cm
(1)如图4-6-1,在△ABC中,DE∥BC,AD=3 cm,BD=2 cm,△ADE与△ABC是否相似________,若相似,相似比是________.

图4-6-1
(2)如图4-6-2,D、E分别为△ABC中AB、AC边上的点,请你添加一个条件,使△ADE与△ABC相似,你添加的条件是_____________(只需填上你认为正确的一种情况即可).
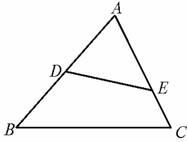
图4-6-2
(3)如图4-6-3,测量小玻璃管口径的量具ABC中,AB的长是10毫米,AC被分成60等份.如果小管口DE正好对着量具上30份处(DE∥AB),那么小管口径DE的长是_____________毫米.
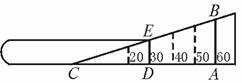
图4-6-3
(4)如图4-6-4,在Rt△ABC中,∠ACB=90°,作CD⊥AB于点D,则图中相似的三角形有________对,它们分别是_____________.
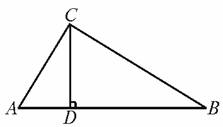
图4-6-4
答:_____________.
通过探索和学习,你知道怎样判定两个三角形相似?那么请把你的判定方法写在下面吧.
(1)_____________.
(2)_____________.
(3)_____________.
2.(1)由△PCD为等边三角形,故∠PCD=∠PDC=60 o,从而∠ACP=∠PBD=120 o,若要△ACP∽△PDB,必要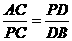 .从而 AC·DB=PC·PD,又PC=PD=CD,故CD2=AC·DB;(2)由△PDB∽△ACD,所以∠A=∠DPB,∠APC=∠B,又因为∠A+∠APC+ACP=180o,故∠A+∠APC=60o,又∠CPD=60o,故∠APB=∠APC+∠BPD+∠CPD=120o
.从而 AC·DB=PC·PD,又PC=PD=CD,故CD2=AC·DB;(2)由△PDB∽△ACD,所以∠A=∠DPB,∠APC=∠B,又因为∠A+∠APC+ACP=180o,故∠A+∠APC=60o,又∠CPD=60o,故∠APB=∠APC+∠BPD+∠CPD=120o
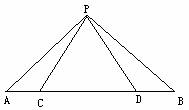
2.如图,点C,D在线段AB上,且△PCD是等边三角形。
(1) 当AC,CD,DB满足怎样的关系时,△ACP∽△PBD;
(2) 当△ACP∽△PBD时,试求∠APB的度数。
答案:1。△AMN∽△CMB, △ABM∽△CEM, △END∽△EBC, △ABN∽△DEN等
1.平行四边形ABCD中,M为对角线AC上一点,BM交AD于N,交CD延长线于E。试问图中有多少对不同的相似三角形?请尽可能多地写出来。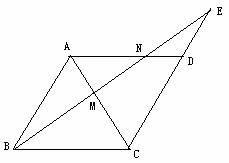
4.3 两个三角形相似的条件 同步练习
创新训练19:
14.某电脑公司现有A、B、C三种型号的甲品牌电脑和D、E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
(1)写出所有选购方案;
(2)如果(1)中各种选购方案被选中的可能性相同,那么A型电脑被选中的概率是多少?
(3)现知希望中学购买甲、乙两种品牌电脑共36台(价格如图2-2-8所示),恰好用了10万元人民币,其中甲品牌电脑为A型电脑,求购买的A型电脑有几台?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com