2、平行投影中的光线是(　　 )

A、平行的　　 　　　　B、聚成一点的　　 　C、不平行的　 　D、向四面八方发散的

1、两个物体的主视图都是圆，则这两个物体可能是(　 )

A、圆柱体、圆锥体　 B、圆柱体、正方体C、圆柱体、球　 D、圆锥体、球

5．如图，一几何体的三视图如右：那么这个几何体是　　　 。　

4．一个四棱锥的俯视图是　　　　　 ；

3．圆柱的左视图是　　　　　　　　 ，俯视图是　　　　　　　　　 ；

2．小华晚上到广场去玩，他发现有两人的影子一个向东，一个向西，于是他肯定的说：“广场上的大灯泡一定位于两人　　　　　　　　　　　 ”；

1．在平行投影中，两人的高度和他们的影子　　　　　　　　　　 ；

13．在Rt△ABC中，∠C=90°，∠A，∠B，∠C的对边分别为a，b，c，根据勾股定理有公式a²+b²=c²，根据三角函数的概念有sinA=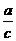，cosA=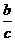，sin²A+cos²A=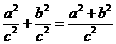=1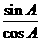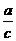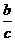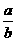，=÷==tanA，其中sin²A+cos²A=1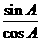，=tanA可作为公式来用．例如，△ABC中，∠C=90°，sinA=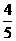，求cosA，tanA的值．

　　 解法一：∵sin²A+cos²A=1；

　　 ∴cos²A=1－sin²A=1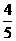－()²=．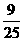

　　 ∴cosA=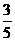，tanA==÷=．

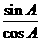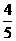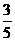　 　解法二：∵∠C=90°，sinA=．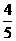

　　 ∴可设BC=4k，AB=5k．

　　 由勾股定理，得AC=3k．

　　 根据三角函数概念，得cosA=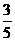，tanA=．

　　 运用上述方法解答下列问题：

　　 (1)Rt△ABC中，∠C=90°，sinA=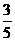，求cosA，tanA的值；

　 　(2)Rt△ABC中，∠C=90°，cosA=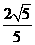，求sinA，tanA的值；

　　 (3)Rt△ABC中，∠C=90°，tanA=，求sinA，cosA的值；

　　 (4)∠A是锐角，已知cosA=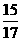，求sin(90°－A)的值．

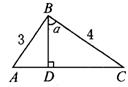
12．如图，在△ABC中，∠ABC=90°，BD⊥AC于D，∠CBD=α，AB=3，BC=4，求sinα，cosα，tanα的值．

◆拓展训练

11．在Rt△ABC中，两边的长分别为3和4，求最小角的正弦值．