
题目列表(包括答案和解析)
1.已知⊙O的半径为5 cm,A为线段OP的中点,当OP=6 cm时,点A与⊙O的位置关系是( )
A.点A在⊙O内 B.点A在⊙O上 C.点A在⊙O外 D.不能确定
4.3两个三角形相似的判定
 第1题. 如图,
第1题. 如图, 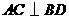 ,垂足为
,垂足为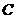 ,过
,过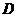 点作
点作 ,垂足为
,垂足为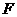 ,交
,交 于
于 点.请找出图中所有的相似三角形,并说明理由.
点.请找出图中所有的相似三角形,并说明理由.
答案:解:(1)因为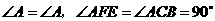
所以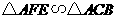 .
.
(2)因为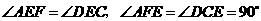 ,
,
所以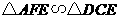 .
.
所以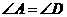 .
.
(3)因为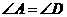 ,
,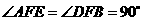 ,
,
所以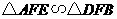 .
.
(4)因为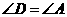 ,
,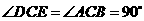 ,
,
所以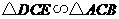 .
.
(5)因为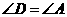 ,
,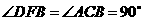 ,
,
所以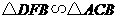 .
.
(6)因为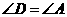 ,
,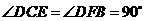 ,
,
所以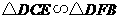 .
.
第2题.  如图,一艘军舰从点
如图,一艘军舰从点 向位于正东方向的
向位于正东方向的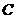 岛航行,在点
岛航行,在点 处测得
处测得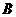 岛在其北偏东
岛在其北偏东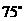 ,航行75n mile到达点
,航行75n mile到达点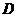 处,测得
处,测得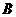 岛在其北偏东
岛在其北偏东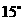 ,继续航行5n mile到达
,继续航行5n mile到达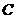 岛,此时接到通知,要求这艘军舰在半小时内赶到正北方向的
岛,此时接到通知,要求这艘军舰在半小时内赶到正北方向的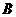 岛执行任务,则这艘军舰航行速度至少为多少时才能按时赶到
岛执行任务,则这艘军舰航行速度至少为多少时才能按时赶到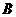 岛?
岛?
答案:解:根据题意,可得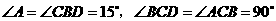 .
.
所以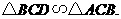
由相似三角形对应边成比例,得
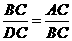 ,即
,即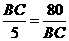 .
.
所以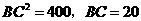 .
.
要求军舰在半小时内赶到正北方向的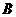 岛执行任务,因此航行速度至少是
岛执行任务,因此航行速度至少是
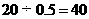 (n
mile/h)
(n
mile/h)
第3题. 如图,点 分别在
分别在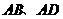 上,
上,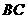 与
与 相交于一点
相交于一点 ,若
,若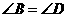 ,
,
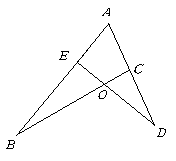 则图中相似三角形有几对?分别写出来说明理由.
则图中相似三角形有几对?分别写出来说明理由.
答案:2对 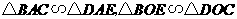 .理由略
.理由略
第4题. 如图,已知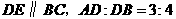 ,若
,若 cm,求
cm,求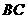 的长.
的长.
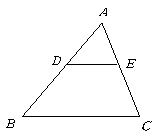
答案: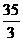 cm
cm
第5题. 如图,已知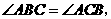 若
若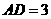 cm,
cm,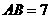 cm,试求
cm,试求 的长.
的长.

答案: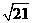 cm
cm
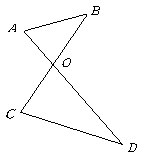
第6题. 如图, 为
为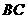 的中点,求
的中点,求 的周长.
的周长.
答案:解:由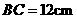 ,
, 为
为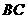 的中点,得
的中点,得
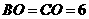 cm.
cm.
由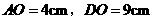 ,得
,得
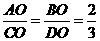 .
.
因为两边对应成比例且夹角相等的两个三角形相似,
所以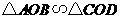 .
.
由相似三角形对应边成比例,得
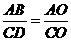 ,即
,即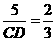 .
.
所以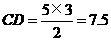 (cm).
(cm).
因此, 的周长是
的周长是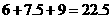 (cm).
(cm).
第7题. 已知 的三条边长之比为
的三条边长之比为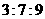 ,与其相似的另一个
,与其相似的另一个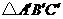 最大的边长为18cm,则
最大的边长为18cm,则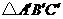 最小的边长为 cm,周长为 cm.
最小的边长为 cm,周长为 cm.
答案:6 38
第8题. 如图,在 中,点
中,点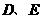 分别在边
分别在边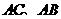 上,且
上,且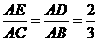 ,若
,若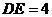 cm,则
cm,则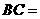 cm.
cm.
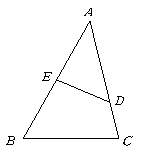
答案:6
第9题. 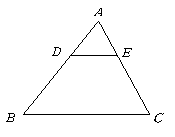 如图,点
如图,点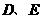 分别为边
分别为边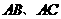 的三等分点(即:
的三等分点(即: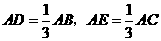 ),若
),若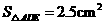 ,求
,求 的大小.
的大小.
答案: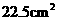
第10题. 如图,在 中,
中,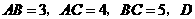 是
是 上的一点,
上的一点,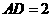 ,在
,在 上是否存在一点
上是否存在一点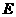 ,使
,使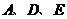 三点组成的三角形与
三点组成的三角形与 相似?如果存在,请求出
相似?如果存在,请求出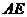 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由. 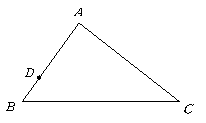
答案:解:存在.
因为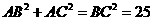 ,
,
所以 是直角三角形,
是直角三角形,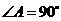 .
.
设所求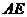 的长为
的长为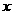 ,
,
在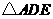 与
与 中,
中, 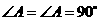 ,
,
(1)若 ,则
,则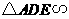
 .
.
此时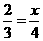 .
.
解得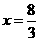 .
.
(2)若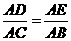 ,则
,则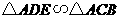 .
.
此时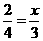 .
.
解得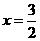 .
.
所以,当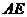 取
取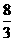 或
或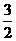 时,
时,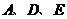 三点组成的三角形与
三点组成的三角形与 相似.
相似.
第11题. 如图,下列条件中不能判定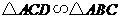 的是( )
的是( )
(A)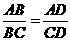 (B)
(B)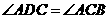
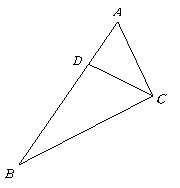 (C)
(C)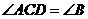 (D)
(D)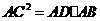
答案:(A)
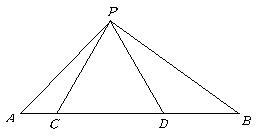
第12题. 已知:如图,点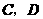 在线段
在线段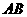 上,
上,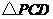 是等边三角形.(1)当
是等边三角形.(1)当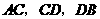 满足怎样的关系式时
满足怎样的关系式时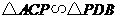 ;(2)当
;(2)当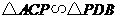 时,求
时,求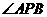 的度数.
的度数.
答案:解:(1)当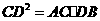 时,
时,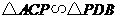 ;
;
(2)当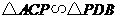 时,
时,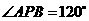 .
.
第13题. 在 和
和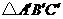 中,
中,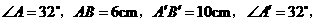
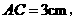
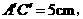 则
则 与
与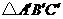 是否相似? (填“是”或“不是”).
是否相似? (填“是”或“不是”).
答案:是
第14题. 下列四组图形中不一定相似的是 .
A.有一个角等于 的两个等腰三角形
的两个等腰三角形
B.有一个角为 的两个直角三角形
的两个直角三角形
C.直角三角形被斜边上的高分成的两个直角三角形
D.有一个角是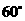 的两个等腰三角形
的两个等腰三角形
答案:A
第15题. 能判定 与
与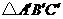 相似的条件是 .
相似的条件是 .
A.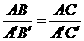 B.
B.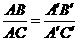 ,且
,且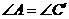
C.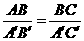 且
且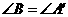 D.
D.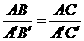 ,且
,且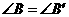
答案:C
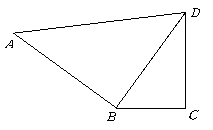 第16题. 已知:如图,
第16题. 已知:如图, ,当
,当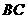 为多少时,图中的两个三角形相似.
为多少时,图中的两个三角形相似.
答案: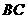 为3.6或4.8
为3.6或4.8
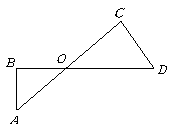 第17题. 如图,线段
第17题. 如图,线段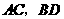 相交于点
相交于点 ,要使
,要使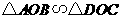 ,已具备条件 ,还需要补充的条件是 ,或 或 .
,已具备条件 ,还需要补充的条件是 ,或 或 .
答案: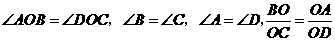
第18题. 如图,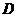 为
为 的边
的边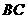 上的一点,连接
上的一点,连接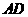 ,要使
,要使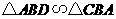 ,应具备下列条件中的( )
,应具备下列条件中的( )
A.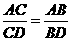 B.
B.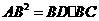
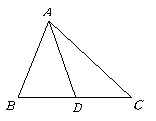 C.
C.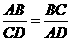 D.
D.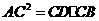
答案:B
第19题. 如图,已知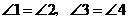 .
.
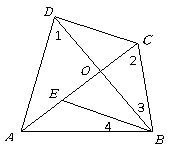 (1)图中有哪几对相似三角形?把它们写出来;
(1)图中有哪几对相似三角形?把它们写出来;
(2)证明你所写出的结论.
答案:(1)解:图中的相似三角形有三对,它们分别是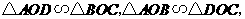
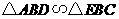
(2)证明: ,
,
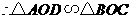 ,
,
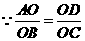 ,即
,即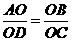 ,
,
又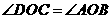 ,
,
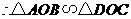
又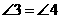 ,
,
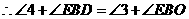
即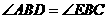
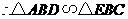 .
.
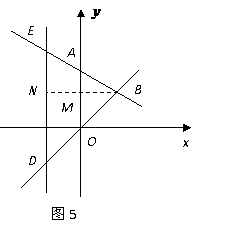
第20题. 如图12,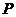 是
是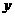 轴上一动点,是否存在平行于
轴上一动点,是否存在平行于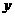 轴的直线
轴的直线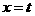 ,使它与直线
,使它与直线 和
和
直线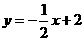 分别交于点
分别交于点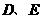 (
(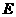 在
在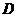 的上方),且
的上方),且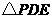 为等腰直角三角
为等腰直角三角
形.若存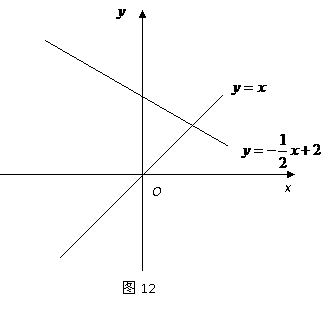 在,求
在,求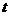 的值及点
的值及点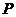 的坐标;若不存在,请说明原因.
的坐标;若不存在,请说明原因.
答案:解:存在.
方法一:当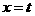 时,
时,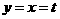 ;当
;当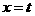 时,
时,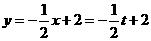 .
.
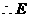 点坐标为
点坐标为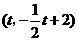 ,
,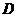 点坐标为
点坐标为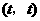 .
.
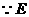 在
在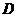 的上方,
的上方,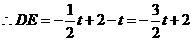 ,且
,且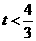 . 3分
. 3分
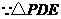 为等腰直角三角形,
为等腰直角三角形,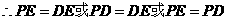 .
.
若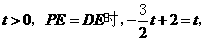
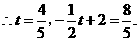
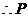 点坐标为
点坐标为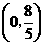 .
.
若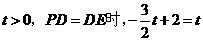 ,
,
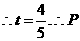 点坐标为
点坐标为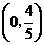 .
.
若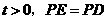 时,即
时,即 为斜边,
为斜边,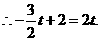
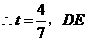 的中点坐标为
的中点坐标为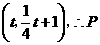 点坐标为
点坐标为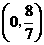 .
.
若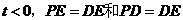 时,由已知得
时,由已知得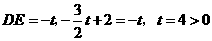
(不符合题意,舍去),
此时直线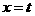 不存在.
不存在.
若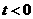 ,
,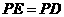 时,即
时,即 为斜边,由已知得
为斜边,由已知得 ,
,
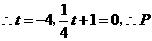 点坐标为
点坐标为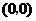 .
.
综上所述:当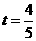 时,
时,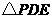 为等腰直角三角形,此时P点坐标为
为等腰直角三角形,此时P点坐标为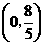 或
或
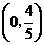 ;当
;当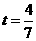 时,
时,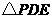 为等腰直角三角形,此时P点坐标为
为等腰直角三角形,此时P点坐标为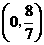 ;
;
当 时,
时,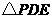 为等腰直角三角形,此时P点坐标为
为等腰直角三角形,此时P点坐标为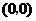 .
.
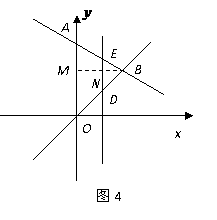
方法二:设直线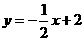 交
交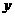 轴于点
轴于点 ,交直线
,交直线 于点
于点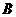 ,过
,过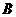 点作
点作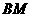
垂直于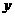 轴,垂足为
轴,垂足为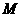 ,交
,交 于点
于点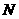 .
.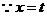 平行于
平行于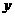 轴,
轴,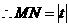 .
.

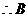 点坐标为
点坐标为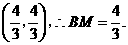 2分
2分
当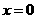 时,
时,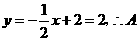 点坐标为
点坐标为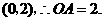 3分
3分
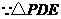 为等腰直角三角形,
为等腰直角三角形,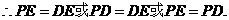
如图4,若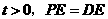 和
和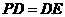 时,
时,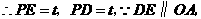
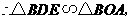
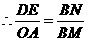 .
.
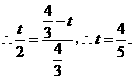
当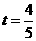 时,
时,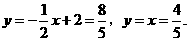
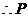 点坐标为
点坐标为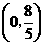 或
或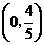 .
.
若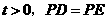 时,即
时,即 为斜边,
为斜边,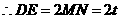 .
.
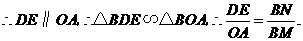
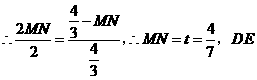 中点的纵坐标为
中点的纵坐标为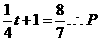 点坐标
点坐标
为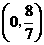
如图5,若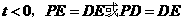 时,
时,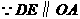 ,
,
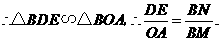
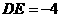 (不符合题意,舍去),此时直线
(不符合题意,舍去),此时直线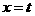 存在. 10分
存在. 10分
若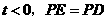 时,即
时,即 为斜边,
为斜边,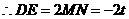
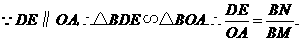
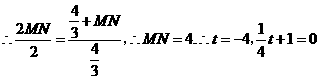
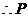 点坐标为(0,0).
点坐标为(0,0).
综上述所述:当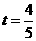 时,
时,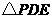 为等腰直角三角形,此时
为等腰直角三角形,此时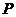 点坐标为
点坐标为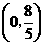 或
或
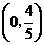 ;当
;当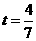 时,
时,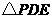 为等腰直角三角形,此时
为等腰直角三角形,此时 点坐标为
点坐标为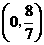 ;当
;当
 时,
时,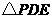 为等腰直角三角形,此时
为等腰直角三角形,此时 点坐标为(0,0).
点坐标为(0,0).
第21题.  如图,
如图,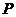 是Rt
是Rt 的斜边
的斜边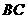 上异于
上异于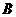 、
、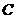 的一点,过
的一点,过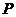
点作直线截 ,使截得的三角形与
,使截得的三角形与 相似,满足这样条件
相似,满足这样条件
的直线共有( )条
A.1 B.2 C.3 D.4
答案:C
第22题. .如图5,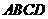 是平行四边形,则图中与
是平行四边形,则图中与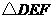 相似的三角形
相似的三角形
 共有( )
共有( )
(A)1个 (B)2分
(C)3个 (D)4个
答案:B
第23题. 如图,梯形ABCD中,AD//BC,BD为对角线,中位线EF交BD于O点,
若FO-EO=3,则BC-AD等于
A.4 B.6 C.8 D.10
 答案:B
答案:B
 第24题. 如图,
第24题. 如图,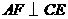 ,垂足为点
,垂足为点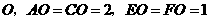 .
.
(1)求证:点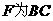 的中点;
的中点;
(2)求四边形 的面积.
的面积.
答案:解:(1)连结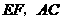


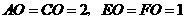 ,
,
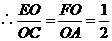 .
.
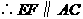 .
.
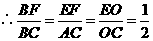 .
.
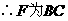 的中点.
的中点.
(2)由(1)知,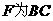 的中点.
的中点.
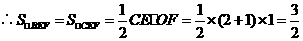 .
.
又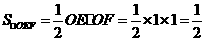 ,
,

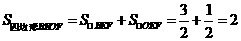
第25题. 小胖和小瘦去公园玩标准的跷跷板游戏,两同学越玩越开心,小胖对小瘦说:“真可惜!
我只能将你最高翘到1米高,如果我俩各边的跷跷板都再伸长相同的一段长度,那么我
就能翘到1米25,甚至更高!”
(1)你认为小胖的话对吗?请你作图分析说明;
(2)你能否找出将小瘦翘到1米25高的方法?试说明.
 解:
解:
答案:解:(1)小胖的话不对.
小胖说“真可惜!我现在只能将你最高翘到1
米高”,情形如图(1)所示,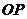 是标准跷跷
是标准跷跷
板支架的高度, 是跷跷板一端能翘到的最
是跷跷板一端能翘到的最
高高度1米,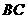 是地面.
是地面.
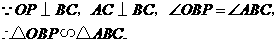
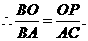
又 此跷跷板是标准跷跷板,
此跷跷板是标准跷跷板, ,
,
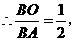 而
而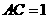 米,得
米,得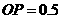 米.
米.
 若将两端同时都再伸长相同的长度,假设为
若将两端同时都再伸长相同的长度,假设为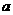 米
米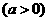 .
.
如图(2)所示,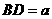 米,
米,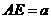 米
米
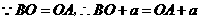 ,即
,即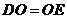 .
.
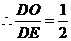 ,同理可得
,同理可得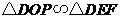 .
.
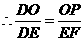 ,由
,由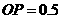 米,得
米,得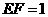 米.
米.

综上所述,跷跷板两边同时都再伸长相同的一段长度,
跷跷板能翘到的最高高度始终为支架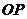 高度的两倍,
高度的两倍,
所以不可能翘得更高.
(2)方案一:如图(3)所示,保持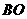 长度不变.将
长度不变.将
 延长一半至
延长一半至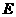 ,即只将小瘦一边伸长一半.
,即只将小瘦一边伸长一半.
使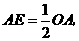 则
则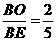 .
.
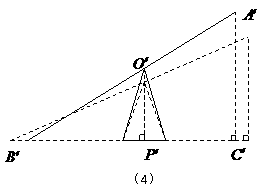 由
由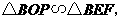 得
得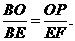
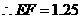 米.
米.
方案二:如图(4)所示,只将支架升高0.125米.
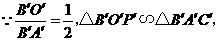
又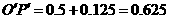 米.
米.
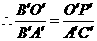 .
.
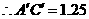 米.
米.
第26题. 在△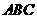 中,
中,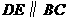 ,
,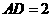 ,
,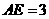 ,
,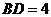 ,则
,则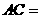 .
.
答案:9
1.两个人轮流在一张桌面(长方形或正方形或圆形)上摆放硬币.规则是每人每次摆一个,硬币不能互相重叠,也不能有一部分在桌面边缘之外,摆好之后不许移动.这样经过多次摆放,直到谁最先摆下硬币谁就认输.按照这个规则你用什么方法才能取胜呢?
7.在等腰三角形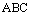 中,
中,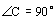 ,
,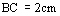 ,如果以
,如果以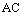 的中点
的中点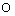 为旋转中心,将这个三角形旋转
为旋转中心,将这个三角形旋转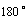 ,点
,点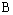 落在
落在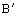 处,那么点
处,那么点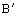 与点
与点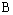 原来位置相距____________.
原来位置相距____________.
综合题
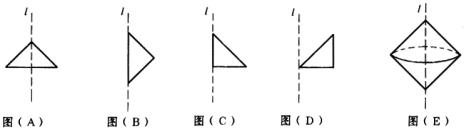
6.如图将三角形绕直线 旋转一周,可以得到图(E)所示的立体图形的是( )
旋转一周,可以得到图(E)所示的立体图形的是( )
A.图(A) B.图(B) C.图(C) D.图(D)
5.等腰三角形、等边三角形、矩形、正方形和圆这五种图形中,既是轴对称图形又是中心对称图形的图形种数是( )
A.2 B.3 C.4 D.5
4.下列图形中不是轴对称图形而是中心对称图形的是( )
A.等边三角形 B.平行四边形 C.矩形 D.菱形
3.国旗上的每个五角星( )
A.是中心对称图形而不是轴对称图形 B.是轴对称图形而不是中心对称图形
C.既是中心对称图形又是轴对称图形 D.既不是中心对称图形,又不是轴对称图形
2.下列说法:(1)平行四边形是中心对称图形,其对角线的交点为对称中心;(2)只有正方形才既是中心对称图形,又是轴对称图形;(3)关于中心对称的两个图形是全等形,两个全等图形也一定成中心对称;(4)若将一个图形绕某定点旋转和另一个图形不重合,那么这两个图形不可能关于这个定点成中心对称,其中正确说法的个数是( )
A.1个 B.2个 C.3个 D.4个
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com