
题目列表(包括答案和解析)
3.把方程(x-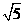 )(x+
)(x+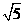 )+(2x-1)2=0化为一元二次方程的一般形式是( )
)+(2x-1)2=0化为一元二次方程的一般形式是( )
A.5x2-4x-4=0 B.x2-5=0 C.5x2-2x+1=0 D.5x2-4x+6=0
2.下列方程:①x2=0,②
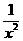 -2=0,③2
-2=0,③2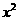 +3x=(1+2x)(2+x),④3
+3x=(1+2x)(2+x),④3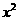 -
-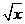 =0,⑤
=0,⑤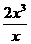 -8x+ 1=0中,
-8x+ 1=0中,
一元二次方程的个数是( )
A.1个 B2个 C.3个 D.4个
1.下列方程中,常数项为零的是( )
A.x2+x=1 B.2x2-x-12=12; C.2(x2-1)=3(x-1) D.2(x2+1)=x+2
23、(11分)如图:抛物线y=x2-2x-3与x轴交 A、B两点(A点在B点左侧),直线1与抛物线交于A、C两点,其中C点的横坐标为2。
A、B两点(A点在B点左侧),直线1与抛物线交于A、C两点,其中C点的横坐标为2。
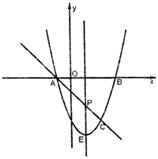
(1)求A、B两点的坐标及直线AC的函数解析式;
(2) P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于
P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于
E点,求线段PE长度的最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,使以A、C、F、G为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标(请直接写出点的坐标,不要求写过程);如果不存在,请说明理由。
23、(11分)云南普洱茶享誉海内外,某茶业有限公司销售一种茶饼,已知每个茶饼的进价为50元,每年销售该茶饼的总开支(不含进价)总计30万元,在销售过程中发现,年销售量y(万个)与销售单价x(元)之间存在如图所示的一次函数关系。
(1)求y与x的一次函数关系式。
(2)写出该公司销售该茶饼的年获利W(万元)关于销售单价x(元)的函数关系式(年获利=年销售额-年销售产品总进价-年总开支)。并求当销售单价x为何值时,年获利最大?
(3)若公司希望该茶饼一年的销售获利不低于20万元,根据(2)中函数的图象,你认为该公司的销售单价应确定在什么范围?在此范围内,要使茶饼的销量最大,你认为销售 单价应定为多少元?


19、(8分)你喜欢玩游戏吗?
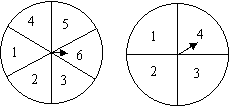
小明和小华在如图所示的两个转盘上玩一个游戏.两个转盘中指针落在每一个数字上的机会都均等,现同时自由转动甲、乙两个转盘,转盘停止后,指针各指向一个数字,若指针停在等分线上,则重转一次,直至指针指向某一数字为止.用所指的两个数字作乘积.如果积为奇数,则小明赢;如果积为偶数,则小华赢,这个游戏公平吗?如果公平,请说明理由;如果不公平,请你做一修改,使他俩获胜的机会一样大.
 20(8分)、如图所示,某幼儿园有一道长为16米的墙,
20(8分)、如图所示,某幼儿园有一道长为16米的墙,
计划用32米长的围栏靠墙围成一个面积为120平方米的
矩形草坪ABCD.求该矩形草坪BC边的长.
21(8分)、如图1是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图2中∠ACB=20°)时最为合适,已知货车车厢底部到地面的距离AB=1.5m,木板超出车厢部分AD=0.5m,请求出木板CD的长度(参考数据:sin20°≈0.3420, cos20°≈0.9397,精确到0.1m).

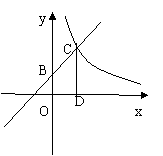 22(9分)、如图,已知一次函数
22(9分)、如图,已知一次函数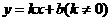 的图象与x轴、y轴
的图象与x轴、y轴
|
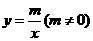 的图象
的图象
在第一象限交于C点,CD垂直与x轴,垂足为D.若OA=OB=OD=1,
(1)求点A,B,D的坐标;
(2)求一次函数和反比例函数的解析式。
18、(7分)如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
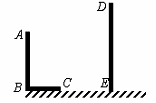 (2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
17、(7分)如图,在四边形ABCD中,AC,BD相交于点O,AB∥CD,AO=CO.
求证:四边形ABCD是平行四边形.
16、(6分)解方程: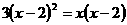
15、观察下列图形,则第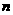 个图形中三角形的个数是
。
个图形中三角形的个数是
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com