
题目列表(包括答案和解析)
4、某商店经销一种销售成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克,销售单价每涨1元,月销售量就减少10千克,针对此回答:
(1)当销售价定为每千克55元时,计算月销售量和月销售利润。
(2)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,
销售单价应定为多少?
3、北京申奥成功,促进了一批产业的迅速发展,某通讯公司开发了一种新型通讯产品投放市场,根据计划,第一年投入资金600万元,第二年比第一年减少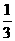 ,第三年比第二年减少
,第三年比第二年减少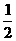 ,该产品第一年收入资金约400万元,公司计划三年内不仅要将投入的总资金全部收回,还要盈利
,该产品第一年收入资金约400万元,公司计划三年内不仅要将投入的总资金全部收回,还要盈利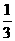 ,要实现这一目标,该产品收入的年平均增长率约为多少?(结果精确到0.1,
,要实现这一目标,该产品收入的年平均增长率约为多少?(结果精确到0.1,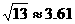 )
)
2、某小组每人送他人一张照片,全组共送了90张,那么这个小组共多少人?
⑴求代数式的值; ⑵解二元二次方程组。
典型例题:
例1、
已知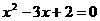 ,求代数式
,求代数式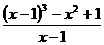 的值。
的值。
例2、如果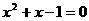 ,那么代数式
,那么代数式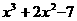 的值。
的值。
例3、已知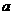 是一元二次方程
是一元二次方程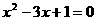 的一根,求
的一根,求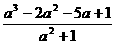 的值。
的值。
例4、用两种不同的方法解方程组
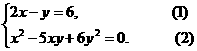
说明:解二元二次方程组的具体思维方法有两种:①先消元,再降次;②先降次,再
消元。但都体现了一种共同的数学思想--化归思想,即把新问题转化归结为我们已
知的问题.
考点四、根的判别式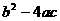
根的判别式的作用:
①定根的个数;
②求待定系数的值;
③应用于其它。
典型例题:
例1、若关于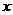 的方程
的方程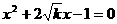 有两个不相等的实数根,则k的取值范围是 。
有两个不相等的实数根,则k的取值范围是 。
例2、关于x的方程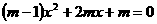 有实数根,则m的取值范围是( )
有实数根,则m的取值范围是( )
A. B.
B.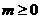 C.
C.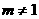 D.
D.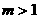
例3、已知关于x的方程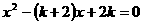
(1)求证:无论k取何值时,方程总有实数根;
(2)若等腰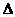 ABC的一边长为1,另两边长恰好是方程的两个根,求
ABC的一边长为1,另两边长恰好是方程的两个根,求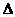 ABC的周长。
ABC的周长。
例4、已知二次三项式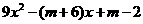 是一个完全平方式,试求
是一个完全平方式,试求 的值.
的值.
例5、 为何值时,方程组
为何值时,方程组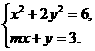 有两个不同的实数解?有两个相同的实数解?
有两个不同的实数解?有两个相同的实数解?
针对练习:
★1、当k
时,关于x的二次三项式 是完全平方式。
是完全平方式。
★2、当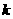 取何值时,多项式
取何值时,多项式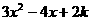 是一个完全平方式?这个完全平方式是什么?
是一个完全平方式?这个完全平方式是什么?
★3、已知方程 有两个不相等的实数根,则m的值是
.
有两个不相等的实数根,则m的值是
.
★★4、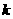 为何值时,方程组
为何值时,方程组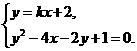
(1)有两组相等的实数解,并求此解;
(2)有两组不相等的实数解;
(3)没有实数解.
★ ★★5、当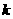 取何值时,方程
取何值时,方程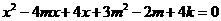 的根与
的根与 均为有理数?
均为有理数?
考点五、方程类问题中的“分类讨论”
典型例题:
例1、关于x的方程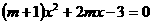
⑴有两个实数根,则m为 ,
⑵只有一个根,则m为 。
例2、
不解方程,判断关于x的方程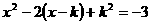 根的情况。
根的情况。
例3、如果关于x的方程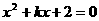 及方程
及方程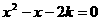 均有实数根,问这两方程
均有实数根,问这两方程
是否有相同的根?若有,请求出这相同的根及k的值;若没有,请说明理由。
考点六、应用解答题
⑴“碰面”问题;⑵“复利率”问题;⑶“几何”问题;
⑷“最值”型问题;⑸“图表”类问题
典型例题:
1、五羊足球队的庆祝晚宴,出席者两两碰杯一次,共碰杯990次,问晚宴共有多少人出席?
⑴条件: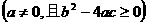
⑵公式: 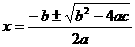 ,
,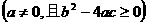
典型例题:
例1、选择适当方法解下列方程:
⑴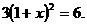 ⑵
⑵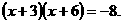 ⑶
⑶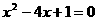
⑷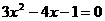 ⑸
⑸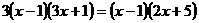
例2、在实数范围内分解因式:
(1)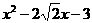 ; (2)
; (2)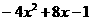 . ⑶
. ⑶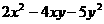
说明:①对于二次三项式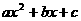 的因式分解,如果在有理数范围内不能分解,
的因式分解,如果在有理数范围内不能分解,
一般情况要用求根公式,这种方法首先令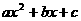 =0,求出两根,再写成
=0,求出两根,再写成
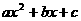 =
= .
.
②分解结果是否把二次项系数乘进括号内,取决于能否把括号内的分母化去.
※在解方程中,多不用配方法;但常利用配方思想求解代数式
的值或极值之类的问题。
典型例题:
例1、
试用配方法说明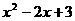 的值恒大于0。
的值恒大于0。
例2、
已知x、y为实数,求代数式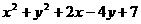 的最小值。
的最小值。
例3、
已知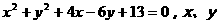 为实数,求
为实数,求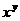 的值。
的值。
例4、
分解因式: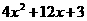
针对练习:
★★1、试用配方法说明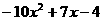 的值恒小于0。
的值恒小于0。
★★2、已知 ,则
,则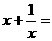 .
.
★★★3、若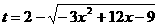 ,则t的最大值为 ,最小值为 。
,则t的最大值为 ,最小值为 。
★★★4、如果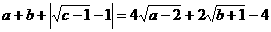 ,那么
,那么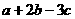 的值为 。
的值为 。
※方程特点:左边可以分解为两个一次因式的积,右边为“0”,
※方程形式:如 ,
,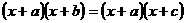 ,
,
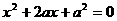
典型例题:
例1、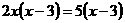 的根为( )
的根为( )
A 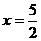 B
B 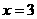 C
C 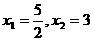 D
D 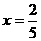
例2、若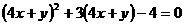 ,则4x+y的值为 。
,则4x+y的值为 。
变式1: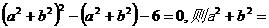 。
。
变式2:若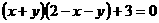 ,则x+y的值为
。
,则x+y的值为
。
变式3:若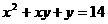 ,
,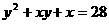 ,则x+y的值为
。
,则x+y的值为
。
例3、方程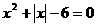 的解为( )
的解为( )
A.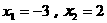 B.
B.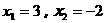 C.
C.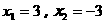 D.
D.
例4、解方程:
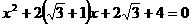
例5、已知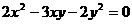 ,则
,则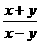 的值为
。
的值为
。
变式:已知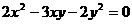 ,且
,且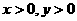 ,则
,则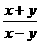 的值为
。
的值为
。
针对练习:
★1、下列说法中:
①方程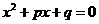 的二根为
的二根为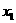 ,
, ,则
,则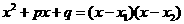
② 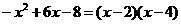 .
.
③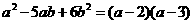
④ 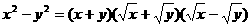
⑤方程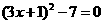 可变形为
可变形为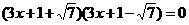
正确的有( )
A.1个 B.2个 C.3个 D.4个
★2、以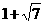 与
与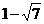 为根的一元二次方程是()
为根的一元二次方程是()
A.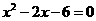 B.
B.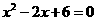
C.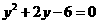 D.
D.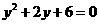
★★3、⑴写出一个一元二次方程,要求二次项系数不为1,且两根互为倒数:
⑵写出一个一元二次方程,要求二次项系数不为1,且两根互为相反数:
★★4、若实数x、y满足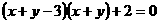 ,则x+y的值为( )
,则x+y的值为( )
A、-1或-2 B、-1或2 C、1或-2 D、1或2
5、方程: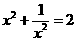 的解是
。
的解是
。
★★★6、已知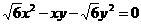 ,且
,且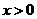 ,
,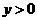 ,求
,求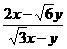 的值。
的值。
★★★7、方程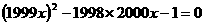 的较大根为r,方程
的较大根为r,方程 的较小根为s,则s-r的值为
。
的较小根为s,则s-r的值为
。
※※对于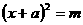 ,
, 等形式均适用直接开方法
等形式均适用直接开方法
典型例题:
例1、解方程: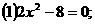
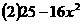 =0;
=0; 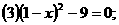
例2、若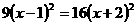 ,则x的值为
。
,则x的值为
。
针对练习:下列方程无解的是( )
A.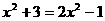 B.
B.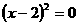 C.
C.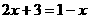 D.
D.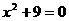
考点一、概念
(1)定义:①只含有一个未知数,并且②未知数的最高次数是2,这样的③整式方程就是一元二次方程。
(2)一般表达式:
⑶难点:如何理解 “未知数的最高次数是2”:
①该项系数不为“0”;
②未知数指数为“2”;
③若存在某项指数为待定系数,或系数也有待定,则需建立方程或不等式加以讨论。
典型例题:
例1、下列方程中是关于x的一元二次方程的是( )
A 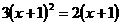 B
B 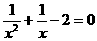
C  D
D 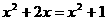
变式:当k
时,关于x的方程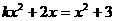 是一元二次方程。
是一元二次方程。
例2、方程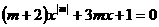 是关于x的一元二次方程,则m的值为 。
是关于x的一元二次方程,则m的值为 。
针对练习:
★1、方程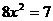 的一次项系数是
,常数项是
。
的一次项系数是
,常数项是
。
★2、若方程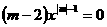 是关于x的一元一次方程,
是关于x的一元一次方程,
⑴求m的值;⑵写出关于x的一元一次方程。
★★3、若方程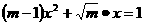 是关于x的一元二次方程,则m的取值范围是 。
是关于x的一元二次方程,则m的取值范围是 。
★★★4、若方程nxm+xn-2x2=0是一元二次方程,则下列不可能的是( )
A.m=n=2 B.m=2,n=1 C.n=2,m=1 D.m=n=1
考点二、方程的解
⑴概念:使方程两边相等的未知数的值,就是方程的解。
⑵应用:利用根的概念求代数式的值;
典型例题:
例1、已知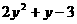 的值为2,则
的值为2,则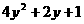 的值为
。
的值为
。
例2、关于x的一元二次方程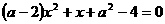 的一个根为0,则a的值为 。
的一个根为0,则a的值为 。
例3、已知关于x的一元二次方程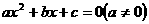 的系数满足
的系数满足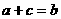 ,则此方程
,则此方程
必有一根为 。
例4、已知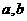 是方程
是方程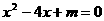 的两个根,
的两个根,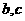 是方程
是方程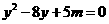 的两个根,
的两个根,
则m的值为 。
针对练习:
★1、已知方程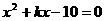 的一根是2,则k为
,另一根是
。
的一根是2,则k为
,另一根是
。
★2、已知关于x的方程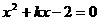 的一个解与方程
的一个解与方程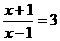 的解相同。
的解相同。
⑴求k的值; ⑵方程的另一个解。
★3、已知m是方程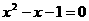 的一个根,则代数式
的一个根,则代数式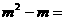 。
。
★★4、已知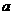 是
是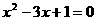 的根,则
的根,则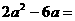 。
。
★★5、方程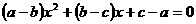 的一个根为( )
的一个根为( )
A 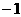 B 1
C
B 1
C 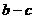 D
D 
★★★6、若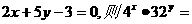 。
。
考点三、解法
⑴方法:①直接开方法;②因式分解法;③配方法;④公式法
⑵关键点:降次
一元二次方程
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com