
题目列表(包括答案和解析)
4. 解:由已知,得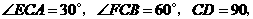
 于点
于点 .
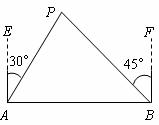
.
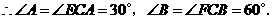
在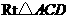 中,
中,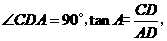
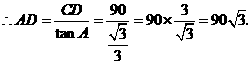
在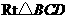 中,
中,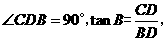
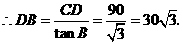
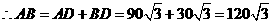 (米).
(米).
答:建筑物 间的距离为
间的距离为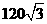 米.
米.
3. 由题意得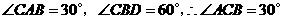 ,
,
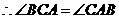 ,
,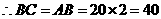 .
.
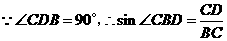 .
.
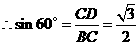 ,
,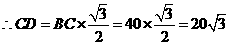 (海里).
(海里).
 此时轮船与灯塔
此时轮船与灯塔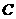 的距离为
的距离为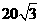 海里.
海里.
2. 解:此方案能够测得该公园的湖心亭A处到南岸的距离.
过点A作南岸所在直线的垂线,垂足是点D,AD的长即为所求.
在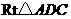 中,∵
中,∵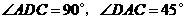 ,∴
,∴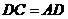
在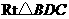 中,∵
中,∵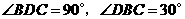 ,∴
,∴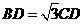
由题意得: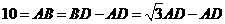 ,解得
,解得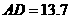
答:该公园的湖心亭A处到南岸的距离约是13.7米.
1. 解:(1)∵OE⊥CD于点E,CD=24,
∴ED = =12.
=12.
在Rt△DOE中,
∵sin∠DOE =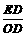 =
=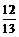 ,
,
∴OD =13(m).
(2)OE=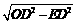 =
=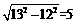 .
.
∴将水排干需: 5÷0.5=10(小时).
5÷0.5=10(小时).
27. 6 28. 4 29. 1 30. 3 31. 1 32 . 1
15. 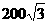 16. 10 17.
16. 10 17. 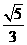 18.
18. 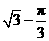 19..
19.. 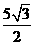 20. 10,
20. 10,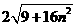 (或
(或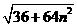 )21.
)21. 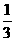 22. 5 23
22. 5 23 。 24。 6
。 24。 6  25. 10m 26. 1.4(或
25. 10m 26. 1.4(或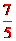 )
)
8. 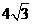 9. 20.3 10. 100 11.
9. 20.3 10. 100 11. 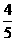 (或0.8); 12.
(或0.8); 12. 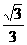 13..
13.. 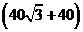 14. 1:2
14. 1:2
1.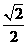 2. 16.1 3. 3.5 4.
2. 16.1 3. 3.5 4. 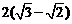 5.
5. 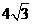 6.
6. 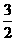 7. 3.5
7. 3.5
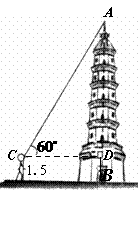
6.(2009河池)如图,为测量某塔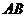 的高度,在离该塔底部20米处目测其
的高度,在离该塔底部20米处目测其 顶A,仰角
顶A,仰角 为
为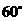 ,目高1.5米,试求该塔的高度
,目高1.5米,试求该塔的高度 .
.

5.(2009年中山)如图所示, .
.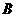 两城市相距
两城市相距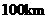 ,现计划在这两座城市间修建一条高速公路(即线段
,现计划在这两座城市间修建一条高速公路(即线段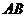 ),经测量,森林保护中心
),经测量,森林保护中心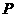 在
在 城市的北偏东
城市的北偏东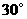 和
和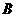 城市的北偏西
城市的北偏西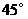 的方向上,已知森林保护区的范围在以
的方向上,已知森林保护区的范围在以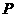 点为圆心,
点为圆心, 为半径的圆形区域内,请问计划修建的这条高速公路会不会穿越保护区,为什么?(参考数据:
为半径的圆形区域内,请问计划修建的这条高速公路会不会穿越保护区,为什么?(参考数据: )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com