15．(1)解一：原方程可化为(x+1)²＝4－4k．　　　　　　　　　　　　　　　 1分

∵该方程有两个不相等的实数根，

∴4－4k＞0．　　　　　　　　　　　　　　　　　　　　　 2分

解得k＜1．

∴k的取值范围是k＜1．　　　　　　　　　　　　　　　　 3分

解二：原方程可化为x²+2x+4k－3＝0．　　　　　　　　　　　　　 1分

＝2²－4(4k－3)＝4(4－4k)．以下同解法一．

(2)解：∵k为非负整数，k＜1，

∴k＝0．　　　　　　　　　　　　　　　　　　　　　　　　　 4分

此时方程为x²+2x＝3，它的根为x₁＝－3，x₂＝1．　　　　　　 5分

14．解：

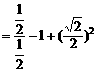　　　　　　　　　　　　　　　　　　　　　　　 4分

　　　　　　　　　　　　　　　　　　　　　　　　　　　　 5分

13．解：因为a＝2，b＝－6，c＝1，　　　　　　　　　　　　　　　　　　 1分

所以b²－4ac＝(－6)²－4×2×1＝28．　　　　　　　　　　　　　 2分

代入公式，得　　　　　　　　　　　　　　 3分

所以原方程的根为(每个根各1分)　　　 5分

25．已知：抛物线与x轴交于点A(x₁，0)、B(x₂，0)，且x₁＜1＜x₂．

(1)求A、B两点的坐标(用a表示)；

(2)设抛物线的顶点为C，求△ABC的面积；

(3)若a是整数，P为线段AB上的一个动点(P点与A、B两点不重合)，在x轴上方作等边△APM和等边△BPN，记线段MN的中点为Q，求抛物线的解析式及线段PQ的长的取值范围．

答案与提示

期末检测题(三)

24．已知：如图，⊙O的内接△ABC中，∠BAC＝45°，∠ABC＝15°，AD∥OC并交BC的延长线于D，OC交AB于E．

(1)求∠D的度数；

(2)求证：AC²＝AD·CE；

(3)求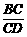的值．

23．已知关于x的方程x²－2ax－a+2b＝0，其中a、b为实数．

(1)若此方程有一个根为2a(a＜0)，判断a与b的大小关系并说明理由；

(2)若对于任何实数a，此方程都有实数根，求b的取值范围．

22．已知：如图，△ABC中，AB＝3，∠BAC＝120°，AC＝1，D为AB延长线上一点，BD＝1，点P在∠BAC的平分线上，且满足△PAD是等边三角形．

(1)求证：BC＝BP；

(2)求点C到BP的距离．

21．某水果批发市场经销一种水果，如果每千克盈利10元，每天可售出500千克．经市场调查发现，在进货价不变的情况下，若每千克这种水果在原售价的基础上每涨价1元，日销售量将减少20千克．

(1)如果市场某天销售这种水果盈利了6 000元，同时顾客又得到了实惠，那么每千克这种水果涨了多少元?

(2)设每千克这种水果涨价x元时(0＜x≤25)，市场每天销售这种水果所获利润为y元．若不考虑其它因素，单纯从经济角度看，每千克这种水果涨价多少元时，市场每天销售这种水果盈利最多?最多盈利多少元?

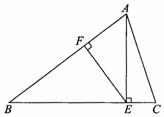
20．已知：如图，等腰△ABC中，AB＝BC，AE⊥BC于E，EF⊥AB于F，若CE＝2，，求EF的长．

19．已知抛物线y＝ax²+bx+c经过点A(0，3)、B(4，3)、C(1，0)．

(1)填空：抛物线的对称轴为直线x＝______，抛物线与x轴的另一个交点D的坐标为______；

(2)求该抛物线的解析式．