16．解：∵在△ABC中，DE∥BC，EF∥AB，

∴∠ADE＝∠B＝∠EFC．

∵DE∥BC，

∴∠AED＝∠C，

∴△ADE∽△EFC．

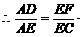
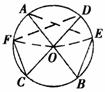
15．证明：连结AE，FD．

∵AB，CD是⊙O的直径．

∴∠AEB＝∠DFC＝90°，AB＝CD．

∵∠C＝∠B．

∴△ABE≌△DCF．

∴FC＝BE．

另证：连结FO，OE

∵∠B＝∠C，

∴∠FOD＝∠EOA有＝．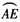

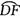∵AB，CD是⊙O的直径，

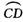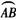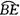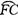∴=．∴＝．∴FC＝BE．

14．解：h＝－5t²+20t＝－5(t²－4t+4)+20＝－5(t－2)²+20

所以，t＝2时，h＝20．

答：当t＝2s时，小球最高，最大高度是20m．

另解：h＝－5t²+20t，a＝－5，b＝20，c＝0．

所以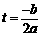，时，h运动到最大高度，即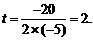

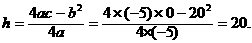
答：当t＝2s时，小球最高，最大高度是20m．

13．解：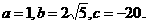

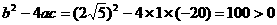
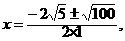
9．120．　 10．k>1．　 11．20．　 12．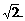

25．如图1，在等腰梯形ABCD中AB∥DC，已知AB＝12，∠DAB＝45°，以AB所在直线为x轴，A为坐标原点建立直角坐标系，将等腰梯形AB－CD绕A点按逆时针方向旋转90°得到等腰梯形OEFG(O、E、F、G分别是A、B、C、D旋转后的对应点)．

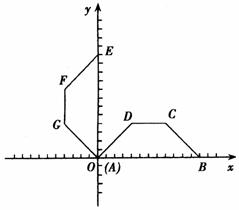
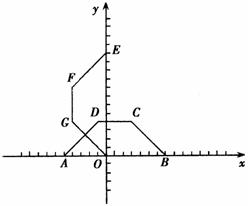
图1　　　　　　　　　　　　　　　　　　　 图2

(1)写出C、F两点的坐标；

(2)将等腰梯形ABCD沿x轴的负半轴平行移动，设移动后的OA的长度是x，如图2，等腰梯形ABCD与等腰梯形OEFG重合部分的面积为y，当点D移动到等腰梯形OEFG的内部时，求y与x之间的函数关系式并写出自变量x的取值范围；

(3)在直线CD上是否存在点P，使△EFP为等腰三角形，若存在，求出P点的坐标，若不存在，说明理由．

答案与提示

期末检测题(一)

24．如图，直角坐标系内的梯形AOBC(O为原点)中AC∥OB，AO⊥OB，AC＝1，OA＝2，OB＝5．

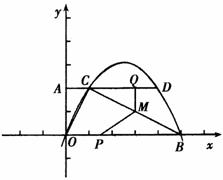
(1)求经过O，C，B三点的抛物线的解析式；

(2)延长AC交抛物线于点D，求线段CD的长；

(3)在(2)的条件下，动点P、Q分别从O、D同时出发，都以每秒1个单位的速度运动，其中点P沿OB由O向B运动，点Q沿DC由D由C运动(其中一个点运动到终点后，另一个点运动也随之停止)，过点Q作QM⊥CD交BC于点M，连结PM．设动点运动的时间为t秒，请你探索：当时间t为何值时，△PMB中有一个角是直角．

23．如图，AB，AC分别是⊙O的直径和弦，D为劣弧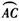上的一点，DE⊥AB于点H，交⊙O于点E，交AC于点F，P为ED的延长线上的一点．

(1)当△PCF满足什么条件时，PC与⊙O相切，用给出的条件证明结论；

(2)当点D在劣弧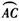的什么位置时，才能使AD²＝DE·DF，请加以证明．

22．某商店销售一批小家电，平均每天可售出20个，每个盈利50元，为扩大销售，增加盈利，减少库存，商场决定采用适当降价的措施．经调查发现，如果每个小家电每降价1元，商店平均每天可多售出2个，若商场平均每天要盈利1600元，每个小家电应降价多少元商店可达到减少库存的目的．

21．如图，在△ABC中，若AB＝5，AC＝2，∠BAC＝120°．以BC为边作等边三角形BCD，把△ABD绕D点按顺时针方向旋转60°到△ECD的位置．

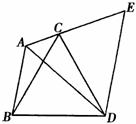
(1)求∠BAD的度数；

(2)求AE的长．