11、已知⊙的半径为2cm，⊙的半径为4cm，圆心距为3cm，则⊙与⊙的位置关系是(　　 )

A. 外离　　　　　 B. 外切　　　　　 C. 相交　　　　　 D. 内切

25．解：(1)过C作CH⊥x轴于点H．

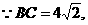∠CBA＝∠DAB＝45°．

∴CH＝HB＝4．

∴C点坐标为(8，4)．

同理可求得F点坐标为(－4，8)．

(2)设AD、CD分别与OG、OE交于点M、N．

∵∠DAB＝∠GOA＝45°，

连结OD，则S_{四边形MOND}＝S_△DMO+S_△DNO，

即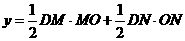

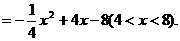
(3)设P点坐标为(a，4)．

①若PE＝PF，

在Rt△PNE和Rt△PGF中，

由PE²＝PN²+NE²＝PG²+FG²＝PF²，

得a²+(12－4)²＝(a+4)²+4²

解得a＝4．

②若PF＝EF．

则由PF²＝PG²+FG²＝EF²，

得

解得a₁＝0，a₂＝－8(舍去)．

③若PE＝EF，

则由PE²＝PN²+NE²＝EF²，

得

化简得a²+32＝0，方程无解，此时P点不存在．

综合①、②、③知，所求P点坐标为P₁(4，4)，P₂(0，4)．

24．解：(1)由题意知，O(0，0)，C(1，2)，B(5，0)．

设过O、C、B三点的抛物线的解析式为y＝ax²+bx，

将C、B点坐标代入y＝ax²+bx，得

可得

(2)当y＝2时，则

解得，x₁＝1，x₂＝4．

∴CD＝4－1＝3．

(3)延长QM交x轴于点N，有MN⊥OB．

①当点P与点N重合时，有

MP⊥OB，则四边形AOPQ是矩形．

∴AQ＝OP即4－t＝t

∴t＝2．

②若MP⊥BM，则△PNM∽△MNB．

∴MN²＝PN·BN．

∵CQ∥NB，

∴△CQM∽△BNM．

即

则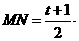

∵BN＝1+t，PN＝5－(1+t)－t＝4－2t，

解得，t₁＝－1(舍去)，

综合①，②知，当t＝2或时，△PMB中有一个角是直角．

23．解：(1)当PC＝PF(或∠PCF＝∠PFC，或△PCF为等边三角形)时，

PC与⊙O相切，下面对满足条件PC＝PF，进行证明

连结OC，则∠OCA＝∠FAO．

∵DE⊥AB于H，PC＝PF，

∴∠AHF＝90°，

∠PCF＝∠PFC．

∵∠AFH＝∠PFC．

∴∠OCA+∠PCF＝∠FAH+∠AFH＝90°．

即OC⊥PC，∴PC与⊙O相切．

(2)当点D是劣弧的中点，AD²＝DE·DF．

连结AE，

∵D点是劣弧的中点，

∴＝

∴∠DAF＝∠DEA．

∵∠ADF＝∠ADE，

∴△ADF∽△EDA．

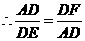，即AD²＝DE·DF．

22．解：设每个小家电应降价x元，根据题意，得

(50－x)(20+2x)＝1600．

即x²－40x+300＝0．

得，x₁＝30，x₂＝10．

因为要尽量减少库存，所以x＝30．

答：每个小家电应降价30元．

21．解：(1)∵把△ABD绕D点按顺时针方向旋转60°，到△ECD位置，

∴∠ADE＝60°，AD＝DE，AB＝CE．

∵∠BAC＝120°，∴∠BAD＝120°－60°＝60°．

(2)由(1)知CE＝AB＝5，AC＝2，∠BAD＝60°，有∠DCE+∠BCD+∠BAC＝180°，

∴AE＝7．

20．(1)由于二次函数图象的顶点是(3，－2)，设所求的二次函数解析式是y＝a(x－3)²－2．由于所求图象过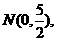

可得

解得所以

列表：

x	…	1	2	3	4	5	…
y	…	0		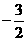－2		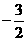0	…

(2)当时，x₁＝1，x₂＝5．

∴点A(1，0)，点B(5，0)，

则 AB＝4．

∵△ABC的面积为12．

∴|h｜＝6．

∴抛物线顶点是(3，－2)．

h₁＝6，h₂＝－6(舍去)．

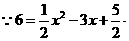
解出，x₁＝7，x₂＝－1．

由于抛物线对称轴是x＝3，

所以x²＝－1(舍去)．有点c(7，6)．

19．解：连结OA．

∵四边形OEPF是正方形，

∴OE⊥AB且平分AB有AE＝EB．

∴OE²+PE²＝OP²有OE＝3cm，

∵OA＝5cm，∴AE²＝OA²－OE²有AE＝4cm．

∵AB＝2AE，∴AB＝8cm．

18．

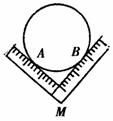
17．方案：(1)L型直角尺两直角边紧靠圆盘，如图所示，图中点A、B表示圆盘与直角尺两直角边的切点．

(2)量出MA的长度，再乘以2就是圆盘的直径．