
题目列表(包括答案和解析)
23.解:
(1)抛物线y = ax2+bx+ c顶点M坐标为(1,2),
 设二次函数解析式为
设二次函数解析式为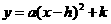

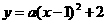 (*)
…………………………(1分)
(*)
…………………………(1分)
 抛物线y = ax2+bx+ c经过坐标原点,
抛物线y = ax2+bx+ c经过坐标原点,
 把(0,0)代入(*)式得:
把(0,0)代入(*)式得: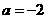
 二次函数解析式为
二次函数解析式为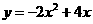 …………………………(3分)
…………………………(3分)
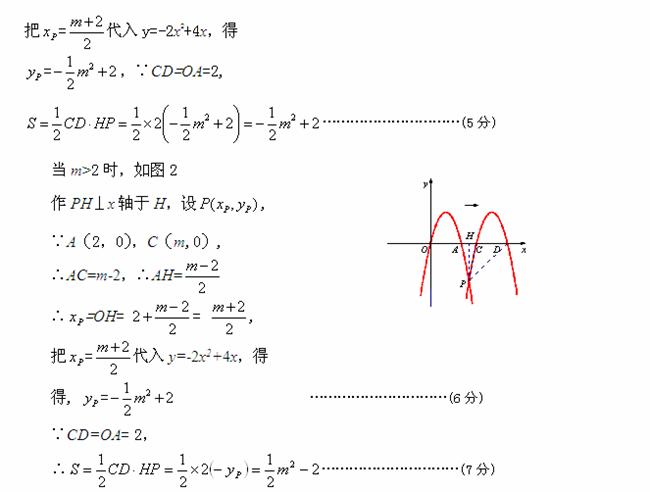
(2)由题意知A点坐标为(2,0)
当0<m<2时,如图1,作PH⊥x轴于点H,设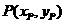 ,
,
∵抛物线向右平移m个单位
∴A(2,0),C(m,0),
∴AC=2-m, ∴CH= 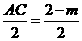 ,…………………………(4分)
,…………………………(4分)
∴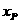 =OH=
=OH= 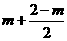 =
= 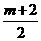 .
.
 (3)根据题意可知:
(3)根据题意可知: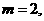
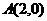 ,
,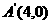
根据勾股定理得: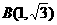
根据三角函数定义知道: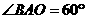

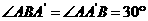
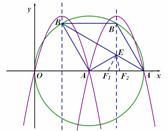 可求得:
可求得: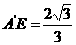 ;
;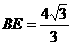
设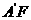 =
=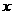
(1) 当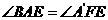

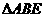 ∽
∽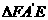

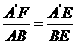
22. 解:
解:

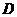 为
为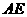 的黄金分割点,
的黄金分割点,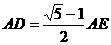

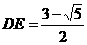 AE………………………(1分)
AE………………………(1分)

20. 解:


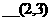 开始
开始
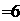
 …………………………(4分)
…………………………(4分)
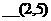
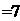
|
|
3 |
4 |
5 |
|
1 |
1+3=4 |
1+4=5 |
1+5=6 |
|
2 |
2+3=5 |
2+4=6 |
2+5=7 |
[错一个扣1分,最多扣四分]
 …………………………(5分)
…………………………(5分)
 …………………………(6分)
…………………………(6分)
 这个方法公平合理。…………………………(7分)
这个方法公平合理。…………………………(7分)
19.解:过点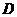 作
作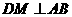 ,垂足为
,垂足为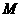
过点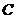 作
作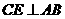 垂足为
垂足为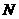 …………………………(1分)
…………………………(1分)
在 中,
中,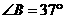

18. 解:由已知得:
解:由已知得: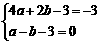 ,…………………………(3分)
,…………………………(3分)
即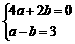 ,解得
,解得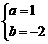 …………………………(5分)
…………………………(5分)
∴所求的二次函数的解析式为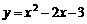 .……………(7分)
.……………(7分)
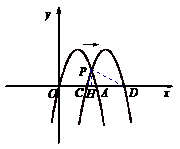
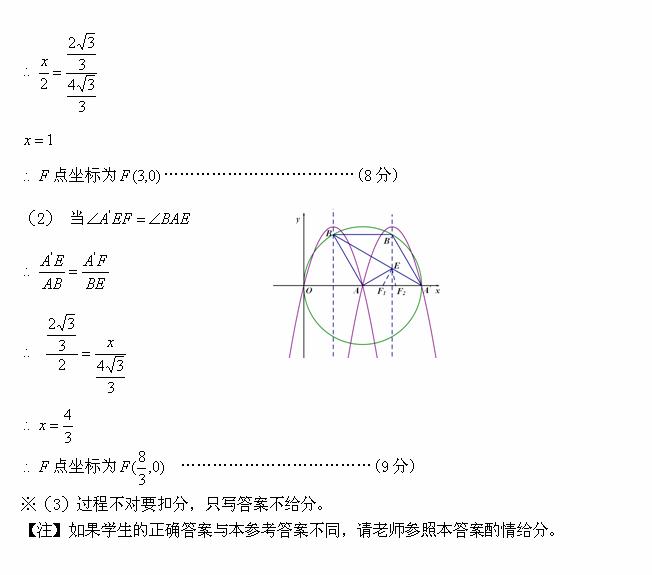
23.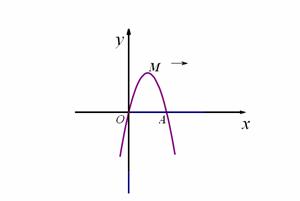 如图①,已知抛物线y = ax2+bx+ c经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
如图①,已知抛物线y = ax2+bx+ c经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
(1)求该抛物线的解析式;
(2)现将它向右平移m(m>0)个单位,所得抛物线
与x轴交于C、D两点,与原抛物线交于点P,△CDP
的面积为S,求S关于m的关系式;
(3)如图②,以点A为圆心,以线段OA为半径画圆, 第23题图①
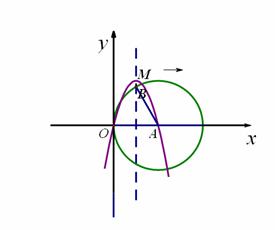 交抛物线y = ax2+bx+ c的对称轴于点B,连结AB,
交抛物线y = ax2+bx+ c的对称轴于点B,连结AB,
若将抛物线向右平移m(m>0)个单位后,B点的对
应点为B′,A点的对应点为A′点,且满足四边形
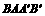 为菱形,平移后的抛物线的对称轴与菱形
为菱形,平移后的抛物线的对称轴与菱形
的对角线BA′交于点E,在x轴上是否存在一点F,
使得以E、F、A′为顶点的三角形与△BAE相似,
若存在求出F点坐标,若不存在说明理由. 第23题图②

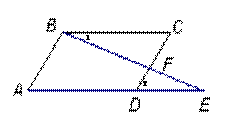
22. 如图,在平行四边形ABCD中,E为边AD延长线上的一点,且D为AE的黄金分割点,即
如图,在平行四边形ABCD中,E为边AD延长线上的一点,且D为AE的黄金分割点,即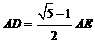 ,BE交DC于点F,已知
,BE交DC于点F,已知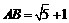 ,求CF的长 .
,求CF的长 .
第22题图
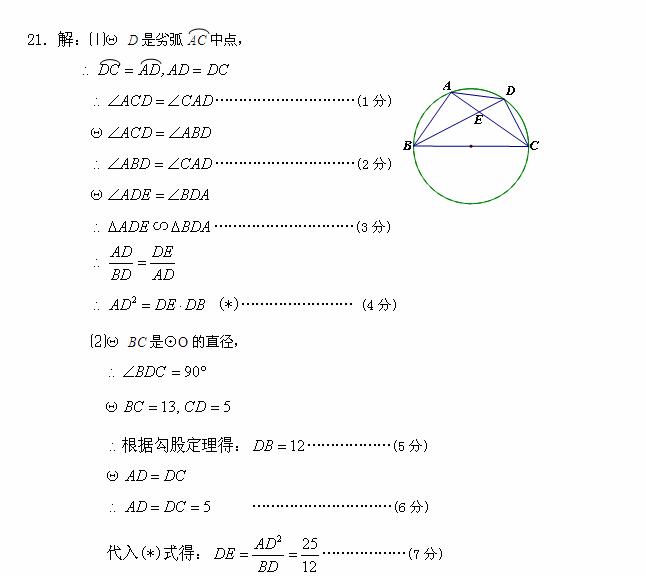
21.如图,⊙O是△ABC的外接圆,BC是⊙O的直径,
|
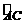 中点,BD交AC于点E.
中点,BD交AC于点E.
⑴求证:AD2=DE·DB
⑵若BC=13,CD=5,求DE的长
第21题图
20.学校奖励给王伟和李丽上海世博园门票共两
张,其中一张为指定日门票,另一张为普通
日门票。王伟和李丽分别转动下图的甲、乙
两个转盘(转盘甲被二等分、转盘乙被三等
分)确定指定日门票的归属,在两个转盘都
停止转动后,若指针所指的两个数字之和为 第20题图
偶数,则王伟获得指定日门票;若指针所指的两个数字之和为奇数,则李丽获得指定日门票;若指针指向分隔线,则重新转动。你认为这个方法公平吗?
 请画树状图或列表,并说明理由.
请画树状图或列表,并说明理由.
19.如图所示,A、B两地之间有一条河,原来从A地到B
地需要经过桥DC,沿折线A→D→C→B到达B地,现
在新建了桥EF,可直接沿直线AB从A地到达B地.
BC=1000m,∠A=45°,∠B=37°.桥DC和AB平行,
则现在从A地到达B地可比原来少走多少路程?(结果
精确到1m.参考数据: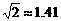 ,sin37°≈0.60,cos37°≈0.80) 第19题图
,sin37°≈0.60,cos37°≈0.80) 第19题图

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com