
题目列表(包括答案和解析)
9、 (08山东聊城)25.(本题满分12分)如图,把一张长10cm,宽8cm的矩形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).
(08山东聊城)25.(本题满分12分)如图,把一张长10cm,宽8cm的矩形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).
(1)要使长方体盒子的底面积为48cm2,那么剪去的正方形的边长为多少?
(2)你感到折合而成的长方体盒子的侧面积会不会有更大的情况?如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由;
(3)如果把矩形硬纸板的四周分别剪去2个同样大小的正方形和2个同样形状、同样大小的矩形,然后折合成一个有盖的长方体盒子,是否有侧面积最大的情况;如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由.
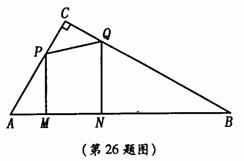
8、(08山东济宁)26.  中,
中,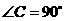 ,
,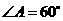 ,
,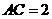 cm.长为1cm的线段
cm.长为1cm的线段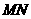 在
在 的边
的边 上沿
上沿 方向以1cm/s的速度向点
方向以1cm/s的速度向点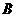 运动(运动前点
运动(运动前点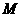 与点
与点 重合).过
重合).过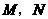 分别作
分别作 的垂线交直角边于
的垂线交直角边于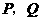 两点,线段
两点,线段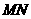 运动的时间为
运动的时间为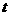 s.
s.
(1)若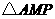 的面积为
的面积为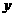 ,写出
,写出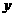 与
与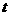 的函数关系式(写出自变量
的函数关系式(写出自变量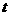 的取值范围);
的取值范围);
(2)线段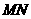 运动过程中,四边形
运动过程中,四边形 有可能成为矩形吗?若有可能,求出此时
有可能成为矩形吗?若有可能,求出此时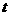 的值;若不可能,说明理由;
的值;若不可能,说明理由;
(3)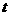 为何值时,以
为何值时,以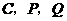 为顶点的三角形与
为顶点的三角形与 相似?
相似?
7、(江苏省镇江市) 22.推理运算
二次函数的图象经过点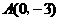 ,
, ,
,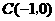 .
.
(1)求此二次函数的关系式;
(2)求此二次函数图象的顶点坐标;
(3)填空:把二次函数的图象沿坐标轴方向最少平移 个单位,使得该图象的顶点在原点.
6、(2008年贵阳市)25.某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
设每个房间每天的定价增加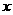 元.求:
元.求:
(1)房间每天的入住量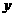 (间)关于
(间)关于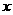 (元)的函数关系式.(3分)
(元)的函数关系式.(3分)
(2)该宾馆每天的房间收费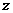 (元)关于
(元)关于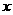 (元)的函数关系式.(3分)
(元)的函数关系式.(3分)
(3)该宾馆客房部每天的利润 (元)关于
(元)关于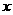 (元)的函数关系式;当每个房间的定价为每天多少元时,
(元)的函数关系式;当每个房间的定价为每天多少元时, 有最大值?最大值是多少?(6分)
有最大值?最大值是多少?(6分)
5、 (2008茂名市)24.我市某工艺厂为配合北京奥运,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价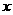 (元∕件) (元∕件) |
…… |
30 |
40 |
50 |
60 |
…… |
每天销售量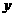 (件) (件) |
…… |
500 |
400 |
300 |
200 |
…… |
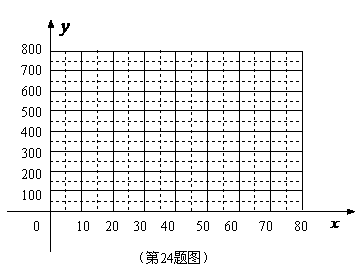 (1)把上表中
(1)把上表中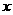 、
、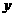 的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想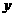 与
与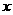 的函数关系,并求出函数关系式;(4分)
的函数关系,并求出函数关系式;(4分)
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)(4分)
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?(2分)
解:
新 课 标第 一网
4、(福建省厦门市2008)24. 已知:抛物线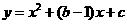 经过点
经过点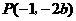 .
.
(1)求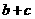 的值;
的值;
(2)若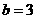 ,求这条抛物线的顶点坐标;
,求这条抛物线的顶点坐标;
(3)若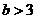 ,过点
,过点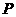 作直线
作直线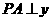 轴,交
轴,交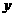 轴于点
轴于点 ,交抛物线于另一点
,交抛物线于另一点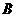 ,且
,且 ,求这条抛物线所对应的二次函数关系式.(提示:请画示意图思考)
,求这条抛物线所对应的二次函数关系式.(提示:请画示意图思考)
3、(莆田市)23.(12分)枇杷是莆田名果之一,某果园有100棵枇杷树。每棵平均产量为40千克,现准备多种一些枇杷树以提高产量,但是如果多种树,那么树与树之间的距离和每一棵数接受的阳光就会减少,根据实践经验,每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量0.25千克,问:增种多少棵枇杷树,投产后可以使果园枇杷的总产量最多?最多总产量是多少千克?
注:抛物线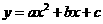 的顶点坐标是
的顶点坐标是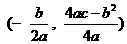
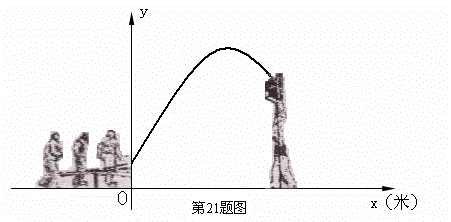
2、(08安徽)杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线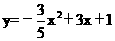 的一部分,如图。
的一部分,如图。
(1)求演员弹跳离地面的最大高度;
[解]
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由。
 [解]
[解]
.
1、(08北京)1、在平面直角坐标系 中,抛物线
中,抛物线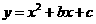 与
与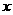 轴交于
轴交于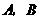 两点(点
两点(点 在点
在点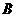 的左侧),与
的左侧),与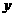 轴交于点
轴交于点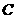 ,点
,点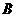 的坐标为
的坐标为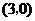 ,将直线
,将直线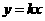 沿
沿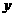 轴向上平移3个单位长度后恰好经过
轴向上平移3个单位长度后恰好经过 两点.
两点.
(1)求直线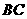 及抛物线的解析式;
及抛物线的解析式;
 (2)设抛物线的顶点为
(2)设抛物线的顶点为 ,点
,点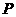 在抛物线的对称轴上,且
在抛物线的对称轴上,且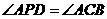 ,求点
,求点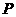 的坐标;
的坐标;
(3)连结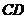 ,求
,求 与
与 两角和的度数.
两角和的度数.
12、. (08德州)7.若A(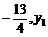 ),B(
),B(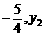 ),C(
),C( )为二次函数
)为二次函数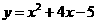 的图象上的三点,则
的图象上的三点,则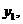
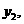
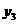 的大小关系是
的大小关系是
A.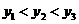 B.
B.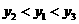
C. D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com