
题目列表(包括答案和解析)
18.(本小题满分8分) ⑴(每对1格给1分,共4分)
|
姓名 |
平均成绩 |
中位数 |
众数 |
方差(S2) |
王 军 军 |
80 |
|
80 |
|
|
李倩 |
|
85 |
|
260 |
⑵李倩 ……………………1分
⑶对于李倩,争取使学习成绩稳定下来,对于王军,争取更好的成绩……3分
17.(本小题满分6分):
解: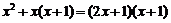 ………………(2分)
………………(2分)
解这个整式方程得: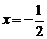 ………………(4分)
………………(4分)
经检验: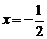 是原方程的解.
是原方程的解.
∴原方程的解为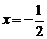 .……………………(6分)
.……………………(6分)
9.-2;10.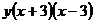 ;11.
;11.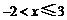 ;12.
;12.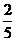 ;13.25; 14.
;13.25; 14. ;15.4; 16.6.
;15.4; 16.6.
3.如果考生在解答的中间过程出现计算错误,但并没有改变试题的实质和难度,其后续部分酌情给分,但最多不超过正确解答分数的一半;若出现严重的逻辑错误,后续部分就不再给分.
2.解答题每小题的解答中所对应的分数,是指考生正确解答到该步骤所应得的累计分数.本答案对每小题只给出一种或两种解法,对考生的其他解法,请参照评分意见进行评分.
1.选择题和填空题中的每小题,只有满分和零分两个评分档,不给中间分.
23. (本题满分12分) 如图,在直角坐标系中,矩形ABCD的边AD在y轴正半轴上,点A、C的坐标分别为(0,1)、(2,4).点P从点A出发,沿A→B→C以每秒1个单位的速度运动,到点C停止;点Q在x轴上,横坐标为点P的横、纵坐标之和.抛物线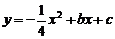 经过A、C两点.过点P作x轴的垂线,垂足为M,交抛物线于点R.设点P的运动时间为t(秒),△PQR的面积为S(平方单位).
经过A、C两点.过点P作x轴的垂线,垂足为M,交抛物线于点R.设点P的运动时间为t(秒),△PQR的面积为S(平方单位).
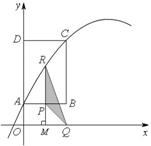 (1)求抛物线对应的函数关系式.
(1)求抛物线对应的函数关系式.
(2)分别求t=1和t=4时,点Q的坐标.
(3)当0<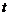 ≤5时,求S与t之间的函
≤5时,求S与t之间的函
数关系式,并直接写出S的最大值.
聊城市二○一一年九年级第一次练兵考试
数学试题参考解答及评分意见
评卷说明:
22.(本题满分10分) 在一平直河岸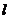 同侧有
同侧有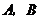 两个村庄,
两个村庄,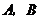 到
到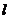 的距离分别是3km和2km,
的距离分别是3km和2km,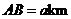
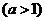 .现计划在河岸
.现计划在河岸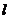 上建一抽水站
上建一抽水站 ,用输水管向两个村庄供水.
,用输水管向两个村庄供水.
方案设计
某班数学兴趣小组设计了两种铺设管道方案:图1是方案一的示意图,设该方案中管道长度为 ,且
,且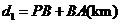 (其中
(其中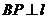 于点
于点 );图2是方案二的示意图,设该方案中管道长度为
);图2是方案二的示意图,设该方案中管道长度为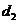 ,且
,且 (其中点
(其中点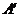 与点
与点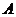 关于
关于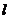 对称,
对称,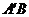 与
与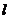 交于点
交于点 ).
).
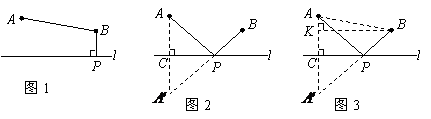
观察计算
(1)在方案一中,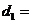 km(用含
km(用含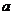 的式子表示);
的式子表示);
(2)在方案二中,组长小宇为了计算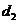 的长,作了如图3所示的辅助线,请你按小宇同学的思路计算,
的长,作了如图3所示的辅助线,请你按小宇同学的思路计算,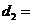 km(用含
km(用含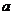 的式子表示).
的式子表示).
探索归纳
(1)①当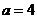 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”);
②当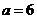 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”);
 (2)请你参考右边方框中的方法指
(2)请你参考右边方框中的方法指
导,就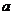 (当
(当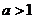 时)的所有取值情况
时)的所有取值情况
进行分析,要使铺设的管道长度较短,
应选择方案一还是方案二?
21. (本题满分10分) 随着人们经济收入的不断提高及汽车产业的快速发展,汽车已越来越多地进入普通家庭,成为居民消费新的增长点.据我市交通部门统计,2007年底我市汽车拥有量为150万辆,而截止到2009年底,我市的汽车拥有量已达216万辆.
(1)求2007年底至2009年底我市汽车拥有量的年平均增长率;
(2)为保护城市环境,缓解汽车拥堵状况,我市交通部门拟控制汽车总量,要求到2011年底全市汽车拥有量不超过231.96万辆;另据估计,从2010年初起,我市此后每年报废的汽车数量是上年底汽车拥有量的10%.假定每年新增汽车数量相同,请你计算出我市每年新增汽车数量最多不能超过多少万辆.
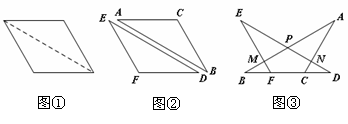
20. (本题满分10分) 如图①,将一个内角为120 的菱形纸片沿较长对角线剪开,得到图②的两张全等的三角形纸片.将这两张三角形纸片摆放成图③的形式.点B、F、C、D在同一条直线上,AB分别交DE、EF于点P、M,AC交DE于点N.
的菱形纸片沿较长对角线剪开,得到图②的两张全等的三角形纸片.将这两张三角形纸片摆放成图③的形式.点B、F、C、D在同一条直线上,AB分别交DE、EF于点P、M,AC交DE于点N.
(1)找出图③中的一对全等三角形(△ABC与△DEF全等除外),并加以证明.
(2)当P为AB的中点时,求△APN与△DCN的面积比.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com