3、用两个全等的直角三角形来拼下列图形，(1)平行四边形(2)矩形　 (3)菱形(4)正方形(5)等腰梯形，一定可以拼成的图形是 (　　 )

A、(1)(2)(5) B、(2)(3)(5)C、(1)(4)(5) D、(1)(2)(3)

2、下列条件中，能判断两个直角三角形全等的是　　　　　　 (­　　 　)

A、两条直角边对应相等　　　　 B、有两条边对应相等

C、一条边和一个锐角对应相等　 D、一条边和一个角对应相等

1、下列图形中,既是中心对称图形，又是轴对称图形的是　　　 (­　　 　)

A、平行四边形­　 B、等边三角形­　　 C、矩形­　　 D、等腰梯形

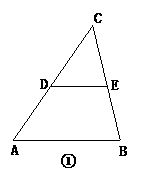
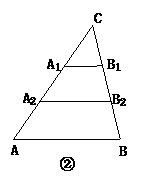
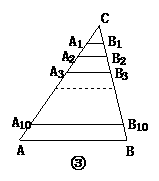
8、已知：△ABC中，AB=10．

(1)如图21①，若点D，E分别是AC，BC边的中点，求DE的长；

(2)如图21②，若点A₁，A₂把AC边三等分，过A₁，A₂作AB边的平行线，分别交BC边于点B₁，B₂，求A₁B₁+A₂B₂的值；

(3)如图21③，若点A₁，A₂，…，A₁₀把AC边十一等分，过各点作AB边的平行线，分别交BC边于点B₁，B₂，…，B₁₀．根据你所发现的规律，直接写出A₁B₁+A₂B₂+…+A₁₀B₁₀的结果．

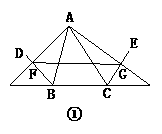
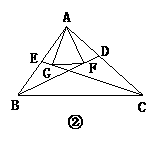
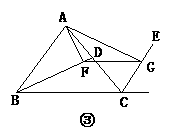
7、已知：如图20①所示，BD、CE分别是△ABC的外角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别为F、G．连结FG，延长AF、AG，与直线BC相交，易证FG=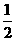(AB+BC+AC)．若(1)BD、CE分别是△ABC的内角平分线(如图②)；(2)BD为△ABC的内角平分线，CE为△ABC的外角平分线(如图③)，则在图②、图③两种情况下，线段FG与△ABC三边又有怎样的数量关系？请写出你的猜想，并对其中的一种情况给予证明．

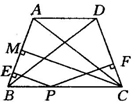
6、如图19，在等腰梯形ABCD中，AD∥BC，AB=DC，P是BC上的一个动点，PE⊥AB，PF⊥CD，CM⊥AB，垂足分别为E、F、M，则PE、PF、CM三者间存在怎样的数量关系？证明你的结论．

5、如图18所示，点E、F分别为正方形ABCD边AB、BC的中点，DF、CE交于点M，CE的延长线交DA的延长线于G，试探索：

(1)DF与CE的位置关系；(2)MA与DG的大小关系．

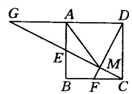
4、已知：如图17所示，平行四边形 ABCD的对角线AC、BD相交于点O，EF经过点O并且分别和AB、CD相交于点E、F，又知G、H分别为OA、OC的中点．

求证：四边形EHFG是平行四边形．

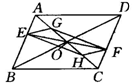
3、如图16，点E是等边△ABC内一点，且EA=EB，△ABC外一点D满足BD=AC，且BE平分∠DBC，求∠BDE的度数．(提示：连接CE)

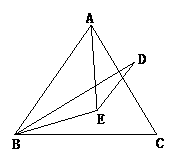
2、如图15，已知点B、C、D在同一条直线上，△ABC和△CDE都是等边三角形．BE交AC于F，AD交CE于H，①求证：△BCE≌△ACD；②求证：CF=CH；③判断△CFH的形状并说明理由．