
题目列表(包括答案和解析)
26、解:(1)∵PC的直线方程为:y=-2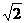 x-8.
x-8.
∴C(-2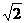 ,0), P(0,-8). ∴|OC|=2
,0), P(0,-8). ∴|OC|=2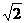 ,|OP|=8,
,|OP|=8,
|PC|= ,
,
|CD|=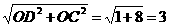 ,
,
|PD|=|OP|+|OD|=8+1=9, PD2=92=81, CD2+PC2=9+72=81.
∴PD2=CD2+PC2 .
∴△DCP为直角三角形,∠DCP=90°,DC⊥PC,CD为直径.
∴PC为⊙D的切线.
(2)设E(r,y),
∴S△OCE=4S△CDO.
∴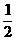 ×|OC|×|y|=4×
×|OC|×|y|=4×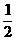 |OC|×|OD|, |y|=4|OD|=4.
|OC|×|OD|, |y|=4|OD|=4.
∴y=±4, E1(-3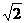 ,4), E2(-
,4), E2(-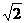 ,-4).
,-4).
25、(1)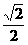 ; (2)
; (2)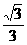 ; (3)
; (3)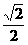 , 1.
, 1.
24、(1)ABC 证明:∵AB为⊙O直径,
∴∠ACB=90°.
∴∠BAC+∠ABC=90°.
若∠CAE=∠ABC. ∴∠BAC+∠CAE=90°,
即∠BAE=90°,OA⊥AE. ∴EF为⊙O的切线.
(2)证明:连接AO并延长交⊙O于点D,
连接CD, ∴∠ADC=∠ABC.
∵AD为⊙O的直径,
∴∠DAC+∠ADC=90°.
∵∠CAE=∠ABC=∠ADC,
∴∠DAC+∠CAE=90°.
∴∠DAE=90°,
即OA⊥EF,EF为⊙O的切线.
23、方法:作一条过圆心与平行四边形对角线交点的直线即把该图形平分,如下图.

22、解:(1)CD是⊙O的切线, 连接OC,BC
∴∠OCA=∠OAC=30°.
∴∠COB=2∠OAC=60°. ∵OC=OB,
∴△OBC为正三角形, 即BC=OB=BD.
∴△OCD是直角三角形,∠OCD=90°,
即OC⊥CD. ∴CD为⊙O的切线.
(2)CD ∵∠OCD=90°,∠COB=60°,
∴∠D=90°-∠COB=30°.
∴∠CAO=∠D, AC=CD.
21、解:作AD⊥BC垂足为D, ∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
∵BC=4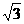 ,
∴BD=
,
∴BD=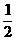 BC=2
BC=2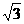 .
可得AD=2.
.
可得AD=2.
又∵⊙A半径为2, ∴⊙A与BC相切.
19、2 6 20、4
15、2π 16、2.4<R<3 17、∠OAC=∠CAE 18、15°
11、2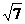 12、2 13、36π
14、4或14
12、2 13、36π
14、4或14
1、A 2、C 3、B 4、A 5、B 6、B 7、D 8、B 9、C 10、A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com