
题目列表(包括答案和解析)
4、到直线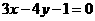 的距离为2的直线方程是. ( )
的距离为2的直线方程是. ( )
A. 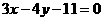 B.
B.
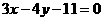 或
或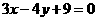
C. 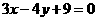 D.
D.
 或
或 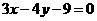
3、设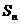 是等差数列
是等差数列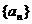 的前n项之和,且
的前n项之和,且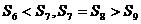 ,则下列结论中错误的是( )
,则下列结论中错误的是( )
A、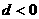 B、
B、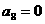 C、
C、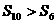 D、
D、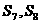 均为
均为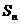 的最大项
的最大项
2、 在△ABC中,b=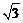 ,c=3,B=300,则a等于( )
,c=3,B=300,则a等于( )
A.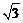 或2
或2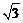 B.2
B.2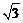 C.
C.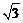 D.2
D.2
1、下列说法正确的是 ( )
(A)若直线l1与l2的斜率相等,则l1//l2
(B)若直线l1//l2,则l1与l2的斜率相等
(C)若一条直线的斜率存在,另一条直线的斜率不存在,则它们一定相交
(D)若直线l1与l2的斜率都不存在,则l1//l2
22.已知整数列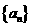 满足
满足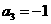 ,
,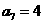 ,前
,前 项依次成等差数列,从第
项依次成等差数列,从第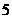 项起依次成等比数列.
项起依次成等比数列.
(1)求数列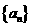 的通项公式;
的通项公式;
(2)求出所有的正整数 ,使得
,使得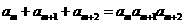 .
.
解:(1) 设数列前6项的公差为d,则a5=-1+2d,a6=-1+3d,d为整数.
又a5,a6,a7成等比数列,所以(3d-1)2=4(2d-1),
即 9d2-14d+5=0,得d =1.
当n≤6时,an =n-4,
由此a5=1,a6=2,数列从第5项起构成的等比数列的公比为2,
所以,当n≥5时,an =2n-5. 故 an =
(2)由(1)知,数列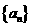 为:-3,-2,-1,0,1,2,4,8,16,…
为:-3,-2,-1,0,1,2,4,8,16,…
当m=1时等式成立,即 -3-2-1=―6=(-3)(-2)(-1);
当m=3时等式成立,即 -1+0+1=0; 当m=2、4时等式不成立;
当m≥5时,amam+1am+2 =23m-12, am +am+1+am+2=2m-5(23-1)=7×2m-5,7×2m-5≠23m-12,
所以 am +am+1+am+2≠amam+1am+2 . 故所求 m= 1,或m=3.
21.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示.
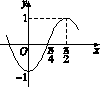
(1)求ω,φ的值;
(2)设g(x)=f(x)f(x-),求函数g(x)的单调增区间.
解:(1)由图可知T=4(-)=π,ω==2,又f(0)=-1,得sinφ=-1,
∵|φ|<π,∴φ=-.
20.在△ABC中,已知B=45°,D是BC边上的一点,AD=10,AC=14,DC=6,求AB的长.
解:在△ADC中,AD=10,AC=14,DC=6,由余弦定理得
cos∠ADC===-,∴∠ADC=120°,∠ADB=60°.
在△ABD中,AD=10,B=45°,∠ADB=60°,由正弦定理得=,
∴AB====5.
19.记等差数列{an}的前n项和为Sn,设S3=12,且2a1,a2,a3+1成等比数列,求Sn.
解:设数列{an}的公差为d.依题设有,即,
解得a1=1,d=3或a1=8,d=-4.
因此Sn=n(3n-1)或Sn=2n(5-n).
18.已知函数f(x)=-sin2x+sinxcosx,x∈R.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在x∈[0,]时的值域.
解:(1)f(x)=-sin2x+sinxcosx=-×+sin2x=sin2x+cos2x-
=sin(2x+)-.∴函数f(x)的最小正周期是T==π.
(2)∵0≤x≤,∴≤2x+≤,∴-≤sin(2x+)≤1,所以f(x)在x∈[0,]的值域为[-,].
11.-1.12.45°.13. .14.
2n2+6n.15.1。16. 2n+1.17. 最大项为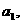 最小项为
最小项为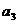 。
。
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com