
题目列表(包括答案和解析)
21.解:(Ⅰ)由圆方程配方得(x+1)2+(y-3)2=9,
圆心为C(-1,3),半径为 r = 3, ……2分
若 l与C相切,则得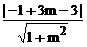 =3, ……4分
=3, ……4分
∴(3m-4)2=9(1+m2),∴m =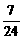 . ……5分
. ……5分
(Ⅱ)假设存在m满足题意。
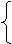 由 x2+y2+2x-6y+1=0 ,消去x得
由 x2+y2+2x-6y+1=0 ,消去x得
x=3-my
(m2+1)y2-(8m+6)y+16=0, ……7分
由△=(8m+6)2-4(m2+1)·16>0,得m>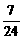 ,
……8分
,
……8分
设A(x1,y1),B(x2,y2),则y1+y2=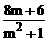 ,y1y2=
,y1y2=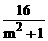 .
.

 OA·OB=x1x2+y1y2
OA·OB=x1x2+y1y2
=(3-my1)(3-my2)+y1y2
=9-3m(y1+y2)+(m2+1)y1y2
=9-3m·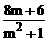 +(m2+1)·
+(m2+1)·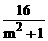
=25- =0 ……12分
=0 ……12分
24m2+18m=25m2+25,m2-18m+25=0,
∴m=9±2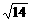 ,适合m>
,适合m>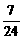 ,
,
∴存在m=9±2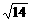 符合要求. ……14分
符合要求. ……14分
18. 解答:解:由2sin(A+B)-=0,得sin(A+B)=, ∵△ABC为锐角三角形
∴A+B=120°, C=60°, 又∵a、b是方程x2-2x+2=0的两根,∴a+b=2,
a·b=2, ∴c2=a2+b2-2a·bcosC=(a+b)2-3ab=12-6=6,
∴c=, S△ABC=absinC=×2×= .

17. 解:(Ⅰ)由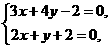 解得
解得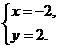
所以点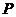 的坐标是
的坐标是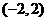 .
……………4分
.
……………4分
(Ⅱ)因为所求直线与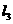 平行,
平行,
所以设所求直线的方程为 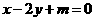 .
.
把点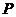 的坐标代入得
的坐标代入得  ,得
,得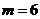 .
.
故所求直线的方程为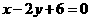 .
……………8分
.
……………8分
(Ⅲ)因为所求直线与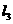 垂直,
垂直,
所以设所求直线的方程为 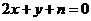 .
.
把点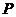 的坐标代入得
的坐标代入得 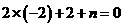 ,得
,得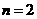 .
.
故所求直线的方程为 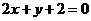 .
……………12分
.
……………12分
21.(本小题满分14分)已知圆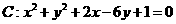 ,直线
,直线 .
.
(Ⅰ)若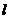 与
与 相切,求
相切,求 的值;
的值;
(Ⅱ)是否存在 值,使得
值,使得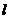 与
与 相交于
相交于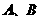 两点,且
两点,且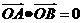 (其中
(其中 为坐标原点),若存在,求出
为坐标原点),若存在,求出 ,若不存在,请说明理由.
,若不存在,请说明理由.

20.(本小题13分)已知直线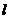 过点P(3,2)且与
过点P(3,2)且与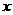 轴正半轴,
轴正半轴,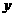 轴正半轴分别交于A、B两点(1)求△AOB面积的最小值及此时直线
轴正半轴分别交于A、B两点(1)求△AOB面积的最小值及此时直线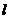 方程(O为原点);
方程(O为原点);
(2)求直线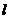 在两坐标轴上截距之和的最小值。
在两坐标轴上截距之和的最小值。
19.(本题满分12分)某公司租赁甲、乙两种设备生产A、B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元.现该公司至少要生产A类产品50件,B类产品140件,问公司租赁甲、乙两种设备各多少台?所需租赁费最少为多少元?
18. (本题满分12分)在锐角三角形中,边a、b是方程x2-2x+2=0的两根,角A、B满足2sin(A+B)-=0,求角C的度数,边c的长度及△ABC的面积.
17. (本小题满分12分)已知直线 :
: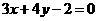 与
与 :
: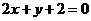 的交点为
的交点为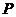 .
.
(Ⅰ)求交点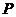 的坐标;
的坐标;
(Ⅱ)求过点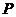 且平行于直线
且平行于直线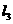 :
: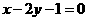 的直线方程;
的直线方程;
(Ⅲ)求过点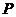 且垂直于直线
且垂直于直线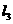 :
: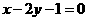 直线方程.
直线方程.
16. (本小题满分12分)
(1)在等差数列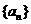 中,
中,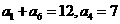 ,求
,求 及前
及前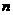 项和
项和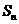 ;
;
(2)在等比数列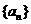 中,
中,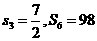 ,求
,求 .
.
15、已知M={(x,y)|x2+y2=1,0<y≤1},N={(x,y)|y=x+b,b∈R},并且M∩N≠Æ,那么b的取值范围是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com