
题目列表(包括答案和解析)
9、数列{an}的通项公式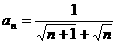 ,已知它的前n项和为Sn=9,则项数n= ( )
,已知它的前n项和为Sn=9,则项数n= ( )
(A)9 (B)10 (C)99 (D)100
8、等差数列{an}中,前三项依次为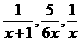 ,则a101=
( )
,则a101=
( )
(A)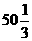 (B)
(B)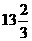 (C)24
(D)
(C)24
(D)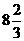
7、等差数列{an} 中,S15=90,则a8= ( )
(A)3 (B)4 (C)6 (D)12
6、设{an}是公差为-2的等差数列,如果a1+ a4+ a7+……+ a97=50,则a3+ a6+ a9……+ a99= ( )
(A)182 (B)-80 (C)-82 (D)-84
5、在等差数列{an}中,公差为d,已知S10=4S5,则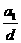 是
( )
是
( )
(A)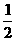 (B)2
(C)
(B)2
(C)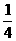 (D)4
(D)4
4、设等差数列的首项为a,公差为d,则它含负数项且只有有限个负数项的条件是 ( )
(A)a>0,d>0 (B)a>0,d<0 (C)a<0,d>0 (D)a<0,d<0
3、含2n+1个项的等差数列,其奇数项的和与偶数项的和之比为 ( )
(A)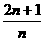 (B)
(B)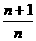 (C)
(C)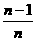 (D)
(D)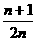
2、等差数列{an}中,a1=3,a100=36,则a3+a98等于 ( )
(A)36 (B)38 (C)39 (D)42
1、若数列{an}的通项公式是an=2(n+1)+3,则此数列 ( )
(A)是公差为2的等差数列 (B)是公差为3的等差数列
(C) 是公差为5的等差数列 (D)不是等差数列
17 (12)已知集合A={x∈R∣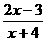 <0},B={ x∈R∣x2+ax+b≤0},
<0},B={ x∈R∣x2+ax+b≤0},
A∩B=ф A∪B={ x∈R∣-4<x≤3}, 求实数a、b的值。
18
(12)用单调性定义证明:f(x)=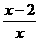 在(-∞,0)上是增函数
在(-∞,0)上是增函数
19(本题满分12分)
设等差数列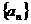 的前n项和为Sn,
的前n项和为Sn,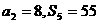 ,数列
,数列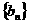 满足
满足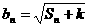 。问是否存在常数k,使数列
。问是否存在常数k,使数列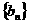 成等差数列?若存在,求出这样的k值;若不存在,说明理由。
成等差数列?若存在,求出这样的k值;若不存在,说明理由。
20(本题满分12分)
我国是水资源比较贫乏的国家之一许多城市采用价格调控等手段,提醒市民节约用水,某市按月收取用户的水费公式是:
水费 = 基本用水费 + 超额用水费 + 定额损耗费
该市规定:
①若月用水量不超过最低限量m立方米,不管用水多少,都需付基本用水费9元和每户每月的定额损耗费a元;
②若月用水量超过m立方米,除了付基本用水费和定额损耗费外,超过部分每立方米付n元的超额用水费。
③用户每月的定额损耗费不超过4元。
(Ⅰ)请写出用户月水费y(元)与月用水量x(立方米)的函数关系式,并注明函数的定义域。
(Ⅱ)该市一用户今年第一季度每月的用水量和支付费用如下表所示:
|
月份 |
用水量(立方米) |
水费(元) |
|
一 |
2.5 |
10 |
|
二 |
3.5 |
14 |
|
三 |
4 |
18 |
请结合上表数值,确定m、n、a的值。
21 (13)已知函数f(x)是定义在(0,∞)的增函数,且f(xy)= f(x)+ f(y)
①
证明:f( )=f(x)- f(y)
)=f(x)- f(y)
② 已知f(3)=1, 且f(a)>f(a-1)+2 ,求a的取值范围。
22.(本题满分14分)
已知一次函数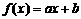 与二次函数
与二次函数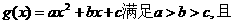
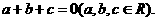
(1)求证:函数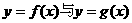 的图象有两个不同的交点A,B;
的图象有两个不同的交点A,B;
(2)设A1,B1是A,B两点在x轴上的射影,求线段A1B1长的取值范围;
(3)求证:当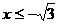 时,
时,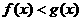 恒成立.
恒成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com