
题目列表(包括答案和解析)
5.设θ∈(0,2π),若sinθ<0,且cos2θ<0,则θ的范围是
A.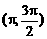 B.
B.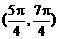 C.
C.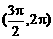 D.
D.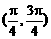
4.在三角形ABC中,已知sinAsinB<cosAcosB,则三角形ABC的形状为
A.锐角三角形 B.直角三角形 C.钝角三角形 D.形状不确定
3.若α为第一象限角,那么sin2α,cosα,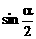 ,
,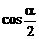 ,中必定取正值的有
,中必定取正值的有
A.0个 B.1个 C.2个 D.3个
2.下列四组角:(1)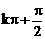 (2)
(2)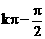 (3)
(3) (4)
(4)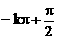
(k∈Z)终边相同的是
A.(1),(2) B.(1),(2),(3)
C.(1),(2),(4) D.(1),(2),(3),(4)
1.Sin600°
A.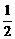 B.
B.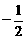 C.
C.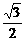 D.
D.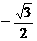
(17)(本小题满分7分)
求函数ƒ(x)=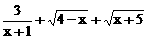 的定义域.
的定义域.
(18)(本小题满分10分)
解不等式:(x+1)( 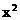 +2x-1) >(x-1)(
+2x-1) >(x-1)( 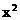 -3).
-3).
(19)(本小题满分12分)
已知集合M={1,3, t},N={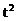 -t+1},若M∪N=M,求t.
-t+1},若M∪N=M,求t.
(20)(本小题满分13分)
函数ƒ(x)=a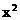 +4x-3,当x∈[0,2]时在x=2取得最大值,求a的取值.
+4x-3,当x∈[0,2]时在x=2取得最大值,求a的取值.
(21)(本小题满分14分)
一条街道上有17户人家,每户的门牌号顺次是1-17.我们假定相邻两户人空的距离相同,都为a.街道上有5个小孩是好朋友,经常聚在一起玩.他们分别住在3、5、7、9、15号。
①设孩子们在门牌号为x(不妨设1≤x≤17,x∈R)的地方聚会,住在9号的小孩到聚会地点所走的路程为y,请写出函数y= ƒ(x)的解析式;
②设孩子们在门牌号为x,(不妨设1≤x≤17,x∈R)的地方聚会,5个小孩到聚会地点所走的总路程为Y,请写出函数Y=F(x)的解析式,并画出函数Y=F(x)的图象简图;请你根据图象,帮助这些孩子在街道上确定一个使他们所走的总路程最小的最佳聚会地点 .
.
(22)(本小题满分14分)
函数ƒ(x)是定义在(-1,1)上的奇函数,
①已知ƒ(x)是单调减函数,求不等式ƒ(1-a)+
ƒ(1-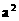 )<0的解;
)<0的解;
②已知ƒ(x)在区间[0,1)上是减函数,证明: ƒ(x)是单调减函数.
(13)设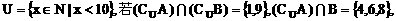 A∩B={2},则A∩(
A∩B={2},则A∩(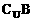 )=_________________________。
)=_________________________。
(14)不等式2<|2x+3|<5的解集是______________________________.
(15)世界人口1992年底达到54.8亿,若人口的年平均增长率为x%,2000年底世界人口数为y亿,那么y与x的函数关系式是______________________.
(16)下列四个命题中,正确的命题是:________________________ (要求把正确的序号都填上)。
①函数y= ƒ(x)和y=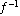 (x)的图象关于直线y=x对称;
(x)的图象关于直线y=x对称;
②函数y= ƒ(x)和x= ƒ(y)的图象关于直线y=x对称;
③函数y= ƒ(x)和x=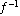 (y)的图象关于直线y=x对称;
(y)的图象关于直线y=x对称;
④函数y= ƒ(x)和x=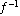 (y)的图象是同一曲线.
(y)的图象是同一曲线.
第Ⅱ卷共70分
(1)设集合A和B都是自然数集合N,映射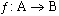 把集合A中的元素n映射到集合B中的元素
把集合A中的元素n映射到集合B中的元素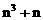 ,则在映射ƒ下,象68的原象是:
,则在映射ƒ下,象68的原象是:
(A)2;(B)3;(C)4;(D)5;
(2)设A={x|x=4k±1,k∈Z},B={x|x=2k+1,k∈Z},则A与B的关系:
(A)A∩B=φ;(B)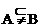 (C)
(C)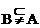 (D)A=B
(D)A=B
(3)下列四组函数中,两函数是同一函数的是:
(A)ƒ(x)= 与ƒ(x)=x;(B) ƒ(x)=
与ƒ(x)=x;(B) ƒ(x)=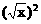 与ƒ(x)
与ƒ(x)
(C) ƒ(x)=x与ƒ(x)=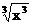 ;(D) ƒ(x)=
;(D) ƒ(x)=  与ƒ(x)=
与ƒ(x)= 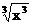 ;
;
(4)命题“若m<0,则方程: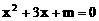 有实根”的
有实根”的 是:
是:
(A)若m>0,则方程: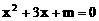 没有实根;
没有实根;
(B)若方程: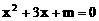 没有实根,则m>0;
没有实根,则m>0;
(C)若方程: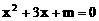 没有实根,则m≥0;
没有实根,则m≥0;
(D)若m≥0,则方程: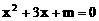 没有实根
没有实根
(5)满足关系式{1}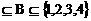 的集合B的个数是:
的集合B的个数是:
(A)6;(B)7;(C)8;(D)9
(6)下列四个命题中,
①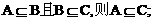 ②
②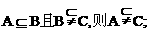
③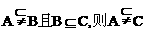 ;④
;④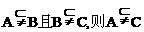 ;
;
正确命题的个数是:
(A)1;(B)2;(C)3;(D)4;
(7)若函数ƒ(x)=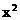 -1(x≤0)的反函数是
-1(x≤0)的反函数是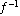 (x),则
(x),则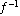 (9)等于:
(9)等于:
(A)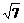 ;(B)
;(B)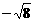 ;(C)3;(D)
;(C)3;(D)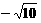
(8)若函数ƒ(2x+1)=3x-1,则函数ƒ(-2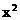 +1)的解析式为:
+1)的解析式为:
(A)-3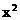 -1;(B)3
-1;(B)3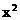 -1;(C)3
-1;(C)3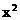 +1;(D)-3
+1;(D)-3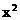 +1
+1
(9)若p:a>2且b>3;q:a+b>5且(a-2)(b-3)>0;则p是q的
(A)充要条件;(B)充分而不必要条件;
(C)必要而不充分条件;(D)既不充分也不必要条件
(10)函数ƒ(x)是偶函数,当x>0时, ƒ(x)=1+2x-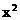 ;则当x<0时, ƒ(x)=
;则当x<0时, ƒ(x)=
(A)1+2x-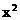 ;(B)1-2x-
;(B)1-2x-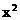 ;(C)1+2x+
;(C)1+2x+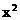 ;(D)1-2x+
;(D)1-2x+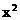
(11)函数ƒ(x)= 的反函数是
的反函数是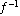 (x)=
(x)=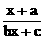 ,则b等于:
,则b等于:
(A)b=2;(B)b=3;(C)b=-2;(D)b=-3
(12)函数ƒ(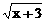 )=
)=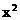 +4x-5,则函数ƒ(x)(x≥0)的值域是:
+4x-5,则函数ƒ(x)(x≥0)的值域是:
(A)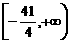 ;(B)
;(B)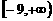 ;(C)
;(C)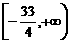 ;(D)
;(D)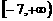
28. 已知二次函数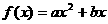 (
(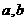 为常数,且
为常数,且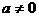 )满足条件:
)满足条件: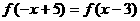 ,且方程
,且方程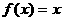 有等根。
有等根。
(1)求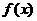 的解析式;
的解析式;
(2)是否存在实数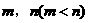 ,使
,使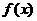 的定义域为
的定义域为 ,值域为
,值域为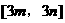 ?如果存在,求出
?如果存在,求出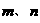 的值;如果不存在,说明理由。
的值;如果不存在,说明理由。
27. 在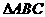 中,记条件
中,记条件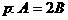 ,条件
,条件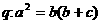 。判断条件
。判断条件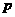 是条件
是条件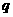 的充分条件,还是必要条件,并证明你的结论。
的充分条件,还是必要条件,并证明你的结论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com