1．对于无穷数列{a_n}，有下列四个命题：

①{a_n}一定有极限；

②若{a_n}是等差数列，那么{a_n}有极限的充要条件是它的公差为0；

③若{a_n}为等比数列，那么当公比q＜1时，{a_n}有极限；

④若{a_n}为递增数列，那么{a_n}一定没有极限．

以上命题中，正确命题的个数是　　　　　　　　　　　　　　　　　　　　　　　　　 [　　 ]

A．0个

B．1个

C．2个

D．3个

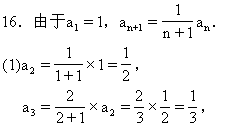
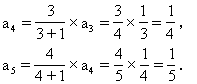
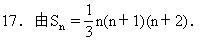
当n=1时，a₁=S₁=2，

当n≥2时，a_n=S_n-S_n-1=n(n+1)．

因为a₁符合n≥2时a_n的解析式，所以数列{a_n}的通项公式为

a_n=n(n+1)．

经检验a₁₁=132，a₁₉=380，而200不是该数列中的项．

18．证明:

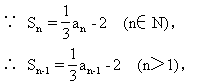
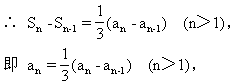
∴　 2a_n+a_n-1=0(n＞1)．

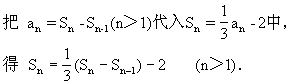
可化简为　 S_n-1+2S_n=-6　　 (n＞1)

14．a₆+a₇=S₇-S₅=2×7³-3×7-2×5³+3×5=430．

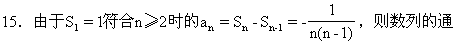
12．a_n+1=a_n²-1．a₁=1，则a₂=a₁²-1=0，a₃=a₂²-1=-1，a₄=a₃²-1=(-1)²-1=0，a₅=a₄²-1=-1．

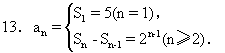
11．数列{a_n}的通项公式为a_n=2n+1．

当n≥2时，b₂=ab₁=aa₁=a₃=7，

b₃=ab₂=a₇=2×7×1=15，

b₄=ab₃=a₁₅=2×15+1=31，

b₅=ab₄=a₃₁=2×31+1=63．

9．由a_n=log_n+1(n+2)，则a₁·a₂·a₃……a₁₄=log₂3×log₃4×log₄5×…×log₁₅16=log₂16=4．

14．430　　　　　　　　　 15．8

提示：

13．5(n-1),2n-1(n≥2)

12．1，0，-1，0，-1

9．4　　　　　　　 10．-2，-8　　　　　　　　　 11．31，63