
题目列表(包括答案和解析)
1.已知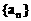 是等比数列,如果
是等比数列,如果 ,那么
,那么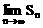 等于( )
等于( )
A.8 B.16 C.32 D.48
21.(Ⅰ)由所给定义及公式有6=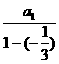 ∴a1=8
∴a1=8
因此S6=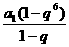 =
=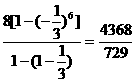
(Ⅱ)由题意:a2=6,S3=21
即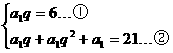
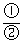 得等式
得等式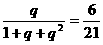 解得q=
解得q=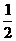 或q=2
或q=2
∴当q=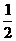 时,该数列为无穷逆缩等比数列,此时a1=12,所有项和S=
时,该数列为无穷逆缩等比数列,此时a1=12,所有项和S=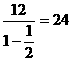
当q=2时,该数列不是无穷逆缩等比数列,此时a1=3,则S10=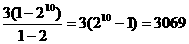
20.(Ⅰ)由题意:a1=2+2×2=6,a2=2+2×2+(2+2×2)=12,∵ a2=a1+a1×1,a3=a2+a2×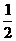 =12+6=18
=12+6=18
 ∴饲养3年后鱼的重量为8万斤。
∴饲养3年后鱼的重量为8万斤。
(Ⅱ)同理:a4=a3+a3 ×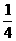 ,a5=a4+a4×
,a5=a4+a4×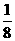 ,…
,…
∴ an=an-1+an-1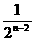 =an-1(1+
=an-1(1+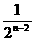 )
)
设第n年鱼的重量最大,则有
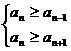 即
即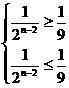
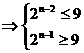
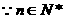 ∴n=5 ∴从第6年(5年后)鱼的重量开始减少。
∴n=5 ∴从第6年(5年后)鱼的重量开始减少。
19. (Ⅰ) f(x) 为奇函数,
f(x) 为奇函数, f(-x)=-f(x)
f(-x)=-f(x)
即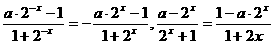
即:a-2x=1=1-a·2x ∴a+a·2x=1+2x,∴a(1+2x)=1+2x∴a=1
(Ⅱ) ∵y=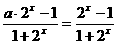 ∴y+y·2x=2x-1
∴y+y·2x=2x-1  2x(y-1)=-1-y,∝2x=
2x(y-1)=-1-y,∝2x=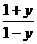 即:f-1(x)=log2
即:f-1(x)=log2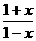 (-1<x<1)
(-1<x<1)
(Ⅲ)log2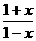 >log2
>log2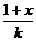 等价于
等价于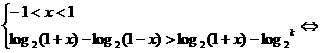
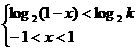
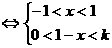

(i)-1<1-k<1,即0<k<2时,{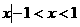 }
}
(ii)1-k -1,即k
-1,即k 2时,{
2时,{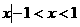 }
}
18.(Ⅰ)设公差为d,则a2=a1+d=8 10a1+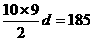
即a1+d=8,2a1+9d=37, ∴a1=5,d=3∴an=a1(n-1)d=3n+2
(Ⅱ)An=a2+a4+a8+…+a2n=(3×2+2)+(3×4+2)+(3×8+2)+ …+(3×2n+2)=3×(2+4+8+…+2n)+2n=3×2n+1+2n-6
17.y=1-2x3在(- ,+
,+ )上为单调减函数。
)上为单调减函数。
证明:任取x1,x2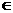 R,且-
R,且- <x1<x2<+
<x1<x2<+
f(x1)-f(x2)=(1-2x31)-(1-2x32)=2(x32-x13)=2(x2-x1)(x22+x1x2+x21)=2(x2-x1)[(x1+x2)2+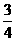 x12] ∵x2>x1∴x0-x1>0,又(x1+x2)2+
x12] ∵x2>x1∴x0-x1>0,又(x1+x2)2+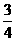 x12>0, ∴f(x1)-f(x2)>0即f(x1)>f(x2)故f(x)=1-2x3在(-
x12>0, ∴f(x1)-f(x2)>0即f(x1)>f(x2)故f(x)=1-2x3在(- ,+
,+ )上为单调减函数。
)上为单调减函数。
13.810 14.1 15.m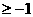 16.x
16.x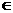 (-
(-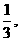 0)
0)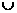 (0,4)
(0,4)
21.(本题满分10分)
给定义等比数列的公比q满足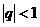 时,称该数列为无穷逆缩等比数列,可以证明这样的数列的所有项的和S=
时,称该数列为无穷逆缩等比数列,可以证明这样的数列的所有项的和S=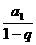
1) 若一个等比数列的所有项的和为6,公比为-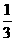 ,求它的前6项的和;
,求它的前6项的和;
20.(本题满分10分)某渔场原有鱼2万斤,所养鱼的重量第一年的增长率为200%,以后每年的增长率都是前一年的一半,问:
1)饲养三年后的鱼的重量是多少;
2)如果因为环境污染,每年损失重量10%,那么经过多少年后鱼的重量开始减少。
19.(本题满分10分)
设函数f(x)=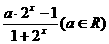 是R上的奇函数。
是R上的奇函数。
(Ⅰ)求a的值;
(Ⅱ)求f(x)的反函数;
(Ⅲ)若k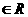 ,解不等于:log2
,解不等于:log2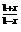 >log2
>log2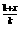
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com