20．设等差数列首项为a₁，公差为d．

由{a_n}为递减数列，则d＜0，可得a₁＝40，d＝-3，a_n=43-3n．

∴a₁＞a₂＞…＞a₁₄＞0＞a₁₅＞…

∴使a_n≥0成立的最大自然数n，能使S_n取最大值，即这个数列前14项和最大，其最大值S₁₄=287．

19．数列{a_n}为首项-60，公差3的等差数列，a_n＝3n-63．

令a_n≤0，即3n-63≤0，n≤21．

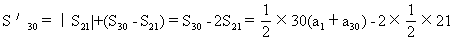
×(a₁+a₂₁)＝765．

18．设等差数列的公差为d，a_n＝a₁+(n-1)d．

解方程，得a₁=-1，d=2或a₁＝3，d＝-2．

∴a_n＝2n-3或a_n＝5-2n．

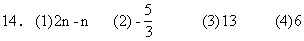
(5)0　　　　　　 (6)900　　　　　　 (7)6　　　　　　 (8)10

15．23　　　　　　　　　 16．113，-22

12．设三边长为12-d，12，12+d，由题意，三角形内切圆半径为3．

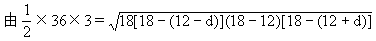
得：d＝±3．

11．题中要找的整数，恰可排列成a₁＝51，公差为10的等差数列，共30项．

8．{a_n}为递减等差数列，若求S_n的最大值，只需求出那些正项的和．

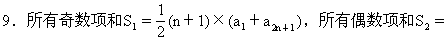
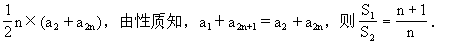
5．2(a+1)=(a-1)+(2a+3)，解得a＝0．

2．利用等差数列的充要条件S_n＝pn²+qn(p，q为常数) 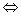{a_n}等差数列．

11．A　　　　　　 12．D

提示：