11．求下列各式的值：

①cos390°+sin2540°+tg120°+ctg270°?

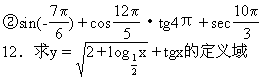
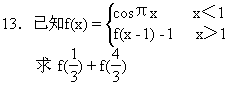
任意角的三角函数·双基能力训练·答案提示

10．已知角α的终边经过点P(4a，-3a)(a≠0)则2sinα+cosα_______．

9．若|ctgx|=-ctgx，则角x的集合是______．

8．若|sinx|=sinx，则角x的集合是______．

6．下列各式为正号的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 [　　 ]

A．cos2-sin2　　　　　　　　　　　　　 B．cos2·sin2

C．tg3·sec2　　　　　　　　　　　　 D．sin2·tg2

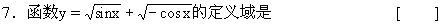
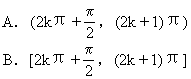
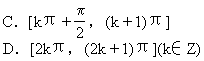
定取正值的有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 [　　 ]

A．0个　　　　　　　　　　　　　 B．1个

C．2个　　　　　　　　　　　　　 D．3个

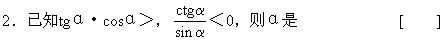
A．第一象限角　　　　　　　　 B．第二象限角

C．第三象限角　　　　　　　　 D．第四象限角

3．设θ是三角形的内角，下列各对数中均取正值的是　　　　　　　　 [　　 ]

A．tgθ和cosθ　　　　　　　　 B．cosθ和cosθ

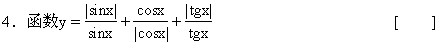
A．{-1，1}　　　　　　　　　　　 B．{-1，1，3}

C．{-1，3}　　　　　　　　　　　 D．{1，3}

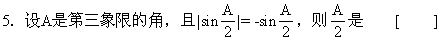
A．第一象限角　　　　　　　　　　　 B．第二象限角

C．第三象限角　　　　　　　　　　　 D．第四象限角

55．已知：sin²Acsc²B+cos²Acos²C=1，求证：tg²Actg²B=sin²C

证：sin²Acsc²B+cos²Acos²C=1

sin²A(ctg²B+1)=1-cos²Acos²C

sin²Actg²B+sin²A=sin²C+cos²C-cos²Acos²C

sin²Actg²B=sin²C+cos²C(1-cos²A)-sin²A

sin²Actg²B=sin²C+cos²Csin²A-sin²A

sin²Actg²B=sin²C+sin²A(cos²C-1)

sin²Actg²B=sin²C-sin²Asin²C sin²Actg²B=sin²Ccos²A

∴tg²Actg²B=sin²C．

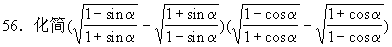
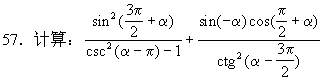
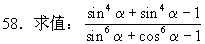
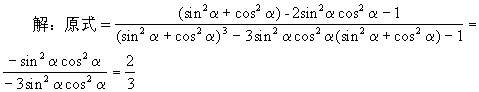
53．求证：csc⁶β-ctg⁶β=1+3csc²βctg²β

证：csc⁶β-ctg⁶β=(csc²β-ctg²β)(csc⁴β+csc²βctg²β+ctg⁴β)=csc⁴β-2csc²βctg²β+ctg⁴β+3csc²βctg²β

=(csc²β-ctg²β)²+3csc²βctg²β=1+3csc²βctg²β．

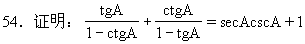
52．证明下列恒等式

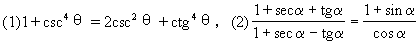
证：(1)∵1-2csc²θ+cos⁴θ=(csc²θ-1)²=(ctg²θ)²=ctg⁴θ

∴1+csc⁴θ=2csc²θ+ctg⁴θ

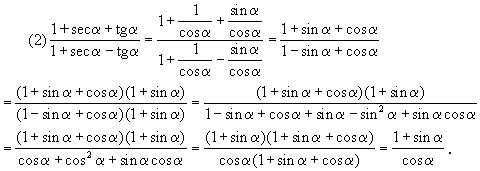
51．已知tg²α=2tg²β+1，求证：sin²β=2sin²α-1

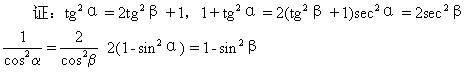
∴sin²β=2sin²α-1．