3．如图在Rt△ABC中，∠C=90°∠B=30°，AB=2，

　 则AC=　　 。

2．=　　　　 　。

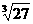1．在实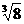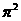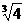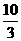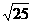数 ，，　 　， ， 　中是　　　　　 无理数 。

10．决策问题类

决策问题，是指根据已掌握的数据及有关信息，利用数学知识对某一事件进行分析、计算，从而作出正确决策的题．

[例12]　 某厂在甲、乙两地的两个分厂各生产某种机器12台和6台，现销售给A地10台，B地8台，已知从甲地调运一台至A地、B地的运费分别为400元和800元，从乙地调运一台至A地、B地的运费分别为300元和500元．

(1)设从乙要调x台至A地，求总运费y关于x轴的函数关系式．

(2)若总运费不超过9000元，问共有几种调运方案？

(3)求出总运费最低的调运方案及最低的运费．

解　 (1)y=300x+500(6－x)+400(10－x)+800[12－(10－x)]=200(x+43)(0≤x≤6，x∈N)

(2)当x=0，1，2时，y≤9000，故共有三种方案，总运费不超过9000元．

(3)在(1)中，当x＝0时，总运费最低，调运方案为：乙地6台全调B地，甲地调2台至B地，10台至A地，这时，总运费y＝8600元．

9．相关学科问题类

这类问题是指涉及相关学科(如物理、化学等)知识的一类数学问题．

[例11]　 在测量某物理量的过程中，因仪器和观察的误差，使得n次测量分别得到a₁，a₂，…，a_n，共n个数据，我们规定所测量的物理量的“最佳近似值”a是这样一个量：与其它近似值比较，a与各数据差的平方和最小，依此规定，求从a₁，a₂，…，a_n推出的a值．

解　 a应满足：y=(a－a₁)²+(a－a₂)²+…+(a－a_n)²

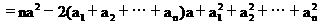
此式表示以a为自变量的二次函数，

∵n＞0．

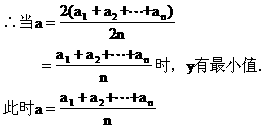
8．增长率(或降低率)问题类

这类问题主要是指工农业生产中计算增长率、产值等方面的一类计算题．

[例10]　 某工厂1988年生产某种产品2万件，计划从1989年开始，每年的产量比上一年增长20%，问哪一年开始，这家工厂生产这种产品的年产量超过12万元(已知lg2＝0.3010，lg3＝0.4771)

解　 设过x年后，产量超过12万件．

则有2(1+20%)^x＞12

解得x＞9.84

答 　从1998年开始年产量可超过12万件．

7．函数模型类

这个问题是指在问题中给出函数关系式，关系式中有的带有需确定的参数，这些参数需要根据问题的内容或性质来确定之后，然后使问题本身获解．

[例8]　 某工厂今年1月、2月、3月生产某产品分别为1万件、1.2万件、1.3万件．为了估测以后每个月的产量，以这三个月的产品数量为依据，用一个函数模拟该产品的月产品的月产量y与月份数x的关系，模拟函数可以选用二次函数或函数y=ab^x+c(其中a、b、c为常数)，已知4月份该产品的产量为1.37万件，请问用以上哪个函数作为模拟函数较好，并说明理由．

解　 设二次函数y₁＝f(x)=px²+qx+x(p≠0)

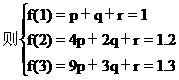
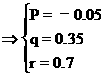
∴y₁=f(x)=－0.05x²+0.35x+0.7

f(4)=－0.05×16+0.35×4+0.7=1.3

又y=ab^x+c

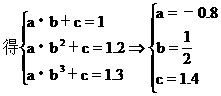
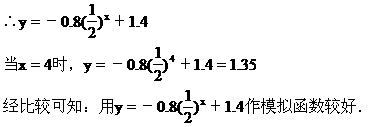
[例9]　 有甲乙两种产品，生产这两种产品所能获得的利润依次

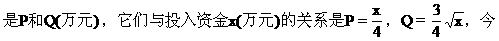
投入3万元资金生产甲、乙两种产品，为获得最大利润，对甲、乙两种产品的资金投入分别应为多少？最大利润是多少？

解 　设投入甲产品资金为x万元，投入乙产品资金为(3－x)万元，总利润为y万元．

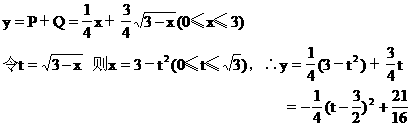
答 　对甲、乙产品分别投资为0.75万元和2.25万元，获最大利润为

6．复利问题类

复利是一种计算利率的方法，即把前一期的利息和本金加在一起做本金，再计算下一期的利息．设本金为P，每期利率为r，设本利和为y，存期为x，则复利函数式为y=P(1+r)^x．

[例7]　 某企业计划发行企业债券，每张债券现值500元，按年利率6.5%的复利计息，问多少年后每张债券一次偿还本利和1000元？(参考lg2=0.3010，lg1.065＝0.0274)．

解 　设n年后每张债券一次偿还本利和1000元，由1000=500(1+6.5%)ⁿ，解得n=lg2/lg1.065≈11．

答 　11年后每张债券应一次偿还本利和1000元．

5．单利问题类

单利是指本金到期后的利息不再加入本金计算．设本金为P元，每期利率为r，经过n期后，按单利计算的本利和公式为S_n=P(1+nR)．

[例6]　 某人于1996年6月15日存入银行1000元整存整取定期一年储蓄，月息为9‰，求到期的本利和为多少？

解 　这里P=1000元，r=9‰，n＝12，由公式得S₁₂＝P(1+12r)＝1000×(1+0.009×12)=1108元．

答 　本利和为1108元．

4．营销问题类

这类问题是指在营销活动中，计算产品成本、利润(率)，确定销售价格．考虑销售活动的盈利、亏本等情况的一类问题．在营销问题中，应掌握有关计算公式：利润=销售价－进货价．

[例5]　 将进货价为8元的商品按每件10元售出，每天可销售200件，若每件售价涨价0.5元，其销售量就减少10件．问应将售价定为多少时，才能使所赚利润最大，并求出这个最大利润．

解　 设每件售价提高x元，则每件得利润(2+x)元，每天销售量变为(200－20x)件，所获利润

y=(2+x)(200－20x)

=－20(x－4)²+720

当x=4时，即售价定为14元时，每天可获最大利润为720元．