
题目列表(包括答案和解析)
[例4] 某鱼塘养鱼,由于改进了饲养技术,预计第一年产量的增长率为200%,以后每年的增长率是前一年增长率的一半,设此鱼塘里原来的鱼储存量为a.
(1)写出改进饲养技术后的第一年、第二年、第三年、第四年的产量,并写出第n年与第(n-1)年(n∈N且n≥2)的产量之间的关系式(不要求证明).
(2)由于环境污染及池塘老化等因素,致使每年将损失年产量的10%,这样以后每年的产量是否始终逐年提高?若是,请予以证明;若不是,请说明从第几年起产量将不如上一年.(lg2=0.3010,lg3=0.4771)
解:(1)不妨设改进技术后第n年的产量为an,则
a1=a(1+200%)=3a,a2=a1(1+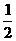 ×200%)=6a,
×200%)=6a,
a3=a2(1+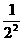 ×200%)=9a,a4=a3(1+
×200%)=9a,a4=a3(1+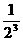 ×200%)=
×200%)=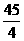 a.
a.
依此,得an=an-1(1+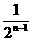 ×200%)=an-1[1+(
×200%)=an-1[1+(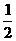 )n-2](n∈N*,n≥2).
)n-2](n∈N*,n≥2).
(2)设遭损失后第n年的产量为bn,则
b1=a1(1-10%),b2=b1(1+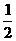 ×200%)(1-10%),…,
×200%)(1-10%),…,
bn=bn-1[1+(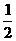 )n-2](1-10%).
)n-2](1-10%).
令bn<bn-1,则0.9[1+(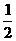 )n-2]<1
)n-2]<1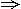 2n-2>9,
2n-2>9,
∴n-2>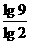 ,即n>5.17.由n∈N*知n≥6.
,即n>5.17.由n∈N*知n≥6.
故从第6年起,产量将不如上一年.
评注:这是一道数列型应用题,审题时应抓住从第二年开始,"以后每年的增长率是前一年增长率的一半"这个关键,把它抽象为数列的通项,容易求出递推关系式an=an-1[1+ (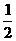 )n-2](n∈N*且n≥2),即建成了递推模型.第(2)问归结为一个指数不等式问题,利用取对数法很容易求得这个数学问题的解.
)n-2](n∈N*且n≥2),即建成了递推模型.第(2)问归结为一个指数不等式问题,利用取对数法很容易求得这个数学问题的解.
●试题详解
高中同步测控优化训练(十一)
第三章 数列(一)(A卷)
说明:本试卷分为第Ⅰ、Ⅱ卷两部分,共100分,考试时间90分钟.
第Ⅰ卷(选择题 共30分)
[例3] 设等差数列{an}的前n项和为Sn,已知a3=12,S12>0,S13<0.
(1)求公差d的取值范围;
(2)指出S1,S2,…,S12中哪一个值最大,并说明理由.
(1)解:依题意有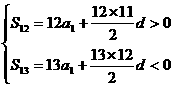
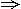
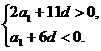
由a3=12,得a1=12-2d.
又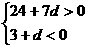
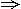 -
-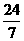 <d<-3.
<d<-3.
(2)解法一:由d<0,可知a1>a2>a3>…>a12>a13.
因此,若在1≤n≤12中,存在自然数n,使得an>0,an+1<0,则Sn就是S1,S2,…,S12中的最大值.
由于S12=6(a6+a7)>0,S13=13a7<0,即a6+a7>0,a7<0,由此得a6>-a7>0.
故在S1,S2,…,S12中S6的值最大.
解法二:Sn=na1+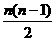 d
d
=n(12-2d)+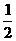 n(n-1)d=
n(n-1)d=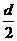 n2-(
n2-(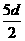 -12)n
-12)n
=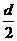 [n-
[n-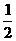 (5-
(5-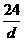 )]2-
)]2-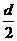 [
[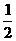 (5-
(5-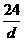 )]2.
)]2.
∵d<0,∴[n-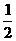 (5-
(5-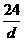 )]2最小时,Sn最大.
)]2最小时,Sn最大.
当-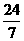 <d<-3时,6<
<d<-3时,6<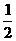 (5-
(5-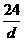 )<6.5.
)<6.5.
∴n=6时,[n-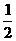 (5-
(5-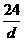 )]2最小.
)]2最小.
∴S6最大.
解法三:由d<0,可知a1>a2>a3>…>a12>a13.
因此,若在1≤n≤12中,存在自然数n,使得an>0,an+1<0,则Sn就是S1,S2,…,S12中的最大值.
由已知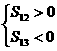
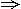
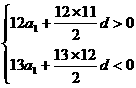
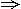
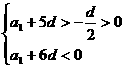
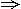

故在S1,S2,…,S12中S6的值最大.
评注:第(2)题用了三种方法来解,解法一与解法三类似,只是确定a6>0,a7<0的方法不同,解法一技巧性强,解法二是把问题转化成了有限制条件的一元二次函数最值问题.
[例2] 已知等差数列{an}为等差数列,p≠q,ap=q,aq=p,求ap+q.
分析:可先转化为a1和d去探索,也可利用等差数列性质求解,还可利用一次函数图象来解.
|
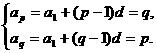
相减得(p-q)d=q-p,∵p≠q,∴d=-1.代入①,
得a1=p+q-1.故ap+q=a1+(p+q-1)d=0.
解法二:ap=aq+(p-q)d,∴q=p+(p-q)d,以下同解法一.
解法三:不妨设p<q,由于an为关于n的一次函数图象上均匀排列的一群孤立点.故(p,ap)、(q,aq)、(p+q,ap+q)三点在同一直线上,如图.
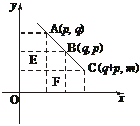
由△ABE∽△BCF得(设ap+q=m)

∴1=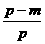 .设m=0,得ap+q=0.
.设m=0,得ap+q=0.
[例1] 等差数列{an}的前n项和记为Sn.已知a10=30,a20=50.
(1)求通项an;
(2)若Sn=242,求n.
分析:在等差数列中,有a1、an、n、d、Sn五个基本量,若已知其中的任何三个,总可以求出另外两个的值.
解:(1)由an=a1+(n-1)d,a10=30,a20=50,
得方程组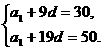
解得a1=12,d=2.
所以an=2n+10.
(2)由Sn=na1+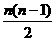 d,Sn=242,得方程12n+
d,Sn=242,得方程12n+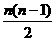 ×2=242.
×2=242.
解得n=11或n=-22(舍去).
评注:本题是一个最基础的数列题,内容上只涉及等差数列的通项和前n项和.它主要考查等差数列的通项公式、求和公式以及构造方程的数学方法,考查运算能力.知识点较为单一,但高考中仍不乏这类考查目的明确、适应所有考生的中低档题.
18、 已知函数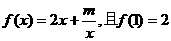 .
.

17、设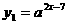 ,
,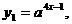 其中
其中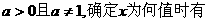
(1)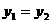 (5分) (2)
(5分) (2)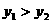 (10分)
(10分)
选做题(20分)
16、设集合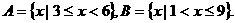
求(1) 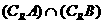 (8分) (2)
(8分) (2)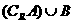 (7分)
(7分)
15、当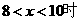 ,
,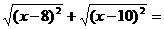 __________
__________
14、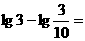 ____________
____________
13、计算机成本不断降低,若每搁3年计算机价格降低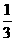 ,现在价格为8100元的计算机,9年后价格可减为___________元
,现在价格为8100元的计算机,9年后价格可减为___________元
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com