1.设数列{a_n}、{b_n}都是等差数列，且a₁=25,b₁=75,a₂+b₂=100,那么由a_n+b_n所组成的数列的第37项为

A.0　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.37

C.100　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.－37

解析：∵{a_n}、{b_n}为等差数列，∴{a_n+b_n}也为等差数列.设c_n=a_n+b_n,则c₁=a₁+b₁=100,而c₂=a₂+b₂=100,故d=c₂－c₁=0.∴c₃₇=100.

答案：C

19.(本小题满分12分)设无穷等差数列{a_n}的前n项和为S_n.

(1)若首项a₁=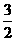,公差d=1,求满足S_k2=(S_k)²的正整数k;

(2)求所有的无穷等差数列{a_n}，使得对一切正整数k都有S_k2=(S_k)²成立.

解：(1)当a₁=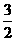,d=1时，

S_n=na₁+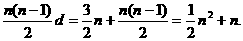

由S_k2=(S_k)²,得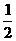k⁴+k²=(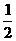k²+k)²,

即k³(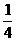k－1)=0.又∵k≠0,∴k=4.

(2)设等差数列{a_n}的公差为d,则在S_k2=(S_k)²中，分别取k=1,2,得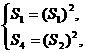

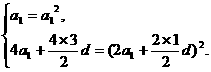
由①得a₁=0或a₁=1.

当a₁=0时，代入②得d=0或d=6.

若a₁=0,d=0,则a_n=0,S_n=0,从而S_k2=(S_k)²成立；

若a₁=0,d=6,则a_n=6(n－1),S_n=3n²－3n.此时S_k2=3k⁴－3k²,(Sk)²=(3k²－3k)²,显然S_k2≠(S_k)².

当a₁=1时，代入②式得d=0或d=2.

若a₁=1,d=0时，a_n=1,S_n=n,从而S_k2=(S_k)²成立；

若a₁=1,d=2时，a_n=2n－1,S_n=1+3+…+(2n－1)=n²,从而S_k2=(S_k)²成立.

综上，共有3个满足条件的无穷等差数列，它们是a_n=0,a_n=1,a_n=2n－1.

18.(本小题满分12分)有30根水泥电线杆，要运往1000米远的地方开始安装，在1000米处放一根，以后每隔50米放一根，一直向前放.一辆汽车一次最多运三根，如果用一辆车完成这项任务，从开始运第一车算起，运完货后回到起点，这辆汽车的行程是多少千米？

解：设在运完第3(n－1)至3n(其中1≤n≤10且n∈N^*)根且返回起点时，这辆汽车的行程为a_n米，则根据题意得a₁=(1000+50+50)×2=2×1100,a₂=(1100+50+50+50)×2=2(1100+150),a₃=(1100+150+50+50+50)×2=2(1100+300),….

∴{a_n}是以2×1100为首项，150为公差的等差数列.从而行程为s₁₀=(1100×10+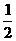×10×9×150)×2=35500.

答：这辆汽车的行程是35500千米.

17.(本小题满分12分)数列的通项公式为a_n=n²－5n+4，问:

(1)数列中有多少项是负数？

(2)n为何值时，a_n有最小值？并求出最小值.

解：(1)由a_n为负数，得n²－5n+4<0,解得1<n<4.

∵n∈N^*,故n=2或3，即数列有2项为负数，分别是第2项和第3项.

(2)∵a_n=n²－5n+4=(n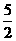－)²－,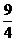

∴对称轴为n=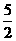=2.5.

又∵n∈N^*,故当n=2或n=3时，a_n有最小值，最小值为2²－5×2+4=－2.

16.(本小题满分10分)已知等差数列{a_n}中，a₁+a₄+a₇=15,a₂a₄a₆=45,求其通项a_n.

解：∵a₁+a₇=2a₄,且a₁+a₄+a₇=15,∴a₄=5.

又∵a₂a₄a₆=45,∴a₂a₆=9.

设其公差为d,又a₄=5,∴a₂=a₄－2d,a₆=a₄+2d.代入a₂a₆=9可得

(5－2d)(5+2d)=9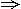25－4d²=9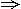d=±2.

当d=2时，a_n=a₄+(n－4)d=5+(n－4)×2=2n－3(n∈N^*);

当d=－2时，a_n=a₄+(n－4)d=5+(n－4)×(－2)=13－2n(n∈N^*).

15.(本小题满分8分)已知数列{a_n}满足下列条件，写出它的前5项，并归纳出数列的一个通项公式.

(1)a₁=0,a_n+1=a_n+(2n－1);

(2)a₁=1,a_n+1=.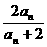

解：(1)∵a₁=0,a_n+1=a_n+(2n－1),

∴a₂=a₁+(2×1－1)=0+1=1,a₃=a₂+(2×2－1)=4,a₄=a₃+(2×3－1)=9,a₅=a₄+(2×4－1)=16.

∴它的前5项依次是0，1，4，9，16.又可写成(1－1)²,(2－1)²,(3－1)²,(4－1)²,(5－1)².

故该数列的一个通项公式是a_n=(n－1)².

(2)∵a₁=1,a_n+1=,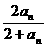

∴a₂=,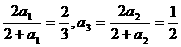

a₄=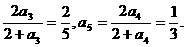

∴它的前5项依次是1,.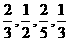

又可写成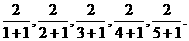

故它的一个通项公式为a_n=.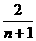

14.等差数列{a_n}中，a₁+a₂+a₃=－24,a₁₈+a₁₉+a₂₀=78,则此数列前20项的和等于________.

解析：由a₁+a₂+a₃=－24,可得3a₂=－24;

由a₁₈+a₁₉+a₂₀=78,可得3a₁₉=78,即a₂=－8,a₁₉=26.

∴S₂₀=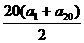=10(a₂₊a₁₉)=10(－8+26)=180.

答案：180

13.在－9和3之间插入n个数，使这n+2个数组成和为－21的等差数列，则n=_______.

解析：－21=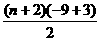,∴n=5.

答案：5

12.若数列{a_n}的前n项和S_n=lg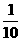［(1+n)］,则a₁₀+a₁₁+a₁₂+…+a₉₉=_________.

解析：a₁₀+a₁₁+…+a₉₉=S₉₉－S₉=lg(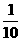·100)－lg(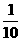·10)=1－0=1.

答案：1

11.设数列{a_n}的前n项和为S_n,S_n=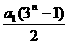(n∈N^*),且a₄=54,则a₁的值是________.

解析：∵a₄=S₄－S₃,

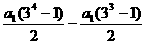∴=54.∴a₁=2.

答案：2