
题目列表(包括答案和解析)
11.等差数列{an}中,a1=-5,它的前11项的平均值是5,若从中抽取1项后余下的10项的平均值仍为5,则抽取的是第_______项.
解析:由-5×11+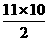 d=55,得d=2.由an=5,an=a1+(n-1)d得n=6.
d=55,得d=2.由an=5,an=a1+(n-1)d得n=6.
答案:6
10.依市场调查结果预测某种家用商品以年初开始的n个月内累积的需求量为Sn(万件),近似地满足Sn=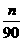 (21n-n2-5)(n=1,2,…,12),则按此预测在本年度内,需求量超过1.5万件的月份是
(21n-n2-5)(n=1,2,…,12),则按此预测在本年度内,需求量超过1.5万件的月份是
A.5月、6月 B.6月、7月
C.7月、8月 D.8月、9月
解析:第n个月需求量an=Sn-Sn-1=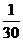 (-n2+15n+9),an>1.5,得
(-n2+15n+9),an>1.5,得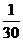 (-n2+15n+9)>1.5.
(-n2+15n+9)>1.5.
解得6<n<9.∴n=7或8.
答案:C
第Ⅱ卷(非选择题 共70分)
9.数列{an}的前n项和Sn=3n-2n2(n∈N*),则当n≥2时,下列不等式中成立的是
A.Sn>na1>nan B.Sn>nan>na1
C.na1>Sn>nan D.nan>Sn>na1
解析:由Sn=3n-2n2可求得an=-4n+5,
∴a1>an(n≥2).
Sn=a1+a2+…+an<na1,
Sn=a1+a2+…+an>nan,
∴nan<Sn<na1.
答案:C
8.已知数列{an}的通项公式为an=(-1) n-1·(4n-3),则它的前100项之和为
A.200 B.-200 C.400 D.-400
解析:S100=a1+a2+…+a100
=1-5+9-13+17-…+(4×99-1)-(4×100-1)
=(1-5)+(9-13)+…+[(4×99-1)-(4×100-1)]
=-4×50=-200.
答案:B
7.若{an}是等差数列,首项a1>0,a2003+a2004>0,a2003·a2004<0,则使前n项和Sn>0成立的最大自然数n是
A.4005 B.4006 C.4007 D.4008
解析:∵a1>0,a2003+a2004>0,a2003·a2004<0,
∴a2003>0,a2004<0.
S4006=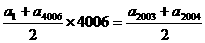 ×4006>0,
×4006>0,
S4007= ×4007=4007×a2004<0.
×4007=4007×a2004<0.
∴使前n项和Sn>0成立的最大自然数n是4006.故选B.
答案:B
6.数列{an}中,a1=1,a2=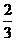 ,且n≥2时,有
,且n≥2时,有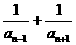 =
=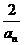 ,则
,则
A.an=(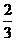 )n B.an=(
)n B.an=(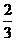 )n-1
)n-1
C.an=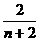 D.an=
D.an=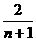
解析:∵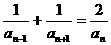 ,n≥2,
,n≥2,
∴数列{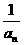 }是等差数列.
}是等差数列.
∵a1=1,a2=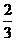 ,
,
∴首项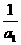 =1,公差d=
=1,公差d=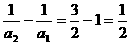 .
.
∴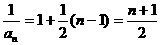 .∴an=
.∴an=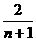 .
.
答案:D
5.数列{an}的通项公式为an=4n-1,令bn=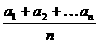 ,则数列{bn}的前n项和为
,则数列{bn}的前n项和为
A.n2 B.n(n+2)
C.n(n+1) D.n(2n+1)
解析:∵an=4n-1,∴数列{an}是等差数列,且a1=4-1=3.
∴bn=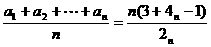 =2n+1.
=2n+1.
显然数列{bn}是等差数列,且b1=2+1=3,
它的前n项和Sn=b1+b2+…+bn=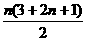 =n(n+2).
=n(n+2).
答案:B
4.在{an}中,a1=15,3an+1=3an-2(n∈N*),则该数列中相邻两项的乘积为负数的项是
A.a21和a22 B.a22和a23
C.a23和a24 D.a24和a25
解析:an+1-an=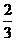 ,∴an=15+(n-1)(-
,∴an=15+(n-1)(-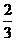 )=
)=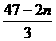 .an+1an<0
.an+1an<0
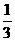 (45-2n)
(45-2n)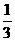 (47-2n)<0
(47-2n)<0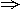
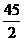 <n<
<n<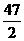 .
.
∴n=23.
答案:C
3.在等差数列{an}中,a1>0,且3a8=5a13,则Sn中最大的是
A.S21 B.S20 C.S11 D.S10
解析:3a8=5a13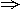 d=-
d=-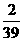 a1<0.an≥0
a1<0.an≥0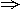 n≤20.
n≤20.
答案:B
2.设{an}为等差数列,则下列数列中,成等差数列的个数为
①{an2} ②{pan} ③{pan+q} ④{nan}(p、q为非零常数)
A.1 B.2 C.3 D.4
解析:{pan}、{pan+q}的公差为pd(设{an}公差为d),而{nan}、{an2}不符合等差数列定义.
答案:B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com