
题目列表(包括答案和解析)
9.  平面上,正三角形ABC与正三角形PQR的面积都为1.三角形PQR的中心M在三角形ABC的边界上,如果这两个三角形重迭部份的面积为S,求S的最小值.
平面上,正三角形ABC与正三角形PQR的面积都为1.三角形PQR的中心M在三角形ABC的边界上,如果这两个三角形重迭部份的面积为S,求S的最小值.
解答:在正△PQR的三个顶点处截去三个全等的正三角形,得到一个面积为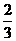 的正六边形,则M是这个正六边形的中心.
的正六边形,则M是这个正六边形的中心.
若点M与△ABC的一个顶点重合,如左图,易知正六边形和△ABC的重迭部分面积是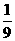 .在中间的图形中,把△ABC绕着点M顺时针旋转,则始边所扫过的三角形和终边所扫过的三角形全等,所以两个三角形的公共部分面积是不变的.
.在中间的图形中,把△ABC绕着点M顺时针旋转,则始边所扫过的三角形和终边所扫过的三角形全等,所以两个三角形的公共部分面积是不变的.
若点M在△ABC的边上,不妨设在BC上,且靠近点C,如右图所示.,过点M作AC的平行线MN,交边AB于点N,则△BMN是正三角形..因为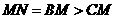 ,BM和MN都与正六边形相交,所以△BMN与正六边形的公共部分面积为
,BM和MN都与正六边形相交,所以△BMN与正六边形的公共部分面积为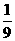 .
.
当把正六边形恢复成原来的正三角形时,公共部分面积不会减小.,所以两个三角形公共部分面积的最小值为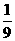 ,如左图.
,如左图.

8. 将正整数中所有被4整除以及被4除余1的数全部删去,剩下的数依照从小到大的顺序排成一个数列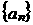
 :2, 3, 6, 7, 10, 11, … .
:2, 3, 6, 7, 10, 11, … .
数列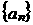 的前n项之和记为
的前n项之和记为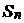 ,其中n=1, 2, 3, ….
,其中n=1, 2, 3, ….
求S=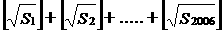 的值.(其中
的值.(其中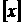 表示不超过x的最大整数)
表示不超过x的最大整数)
解答:易知 ,
,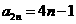 ,
,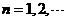 ,因此
,因此
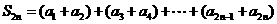
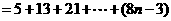
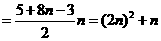 ,
,
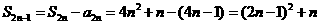 ,
,
所以
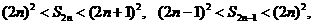
故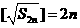 ,
,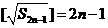 ,从而
,从而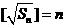 ,于是
,于是
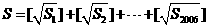
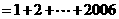
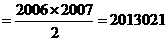 .
.
7. 设n为任意奇正整数,证明: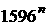 +
+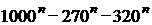 能被2006整除.
能被2006整除.
证明:因为
 ,所以为证结论成立,只需证
,所以为证结论成立,只需证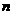 为奇正整数时,
为奇正整数时,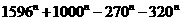 能被2,17,59整除.显然,表达式能被2整除.
能被2,17,59整除.显然,表达式能被2整除.
应用公式,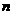 为奇数时,
为奇数时,
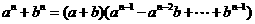 ,
,
 .
.
则由于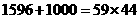 ,
,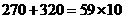 ,所以
,所以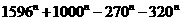 能被59整除.
能被59整除.
又1596-270=1326=17×78,1000-320=680=17×40,所以 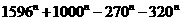 能被17整除.
能被17整除.
故结论成立.
6. 甲和乙在一个n´n的方格表中做填数游戏,每次允许在一个方格中填入数字0或者1(每个方格中只能填入一个数字),由甲先填,然后轮流填数,直至表格中每个小方格内都填了数.如果每一行中各数之和都是偶数,则规定为乙获胜,否则当作甲获胜.请问:
(1) 当n=2006时,谁有必胜的策略?
(2) 对于任意正整数n,回答上述问题.
解答:(1) 当n=2006时,后填数的乙有必胜策略.用1´2的多米诺骨牌对表格进行分割,使得每一行都由1003块多米诺组成,当甲对某块多米诺的一个中填数时,乙也在该多米诺中填数,并且使得这块多米诺中两个数之和为偶数.依此策略,乙可以使得表格的每一行中各数之和都是偶数.故乙获胜.
(2) 当n为偶数时,同上述操作,可知乙有必胜策略;当n为奇数时,甲有必胜策略:他可以先在第1行第1列的方格中写上1,然后对第1行中其余方格作前面的多米诺分割,采取同样的操作方式,可使表格中第1行中各数之和为奇数.
5. “幸运数”是指一个等于其各位数码 (十进制) 和的19倍的正整数,求出所有的幸运数.
解答:设10 a+b是一个至多两位数,方程 10 a + b = 19 (a + b) 仅当 a = b = 0时成立.所以,所有的幸运数至少是三位数.
假设一个幸运数有m位数,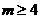 ,则该数至少为
,则该数至少为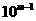 ,其数码和至多为 9m,所以,
,其数码和至多为 9m,所以,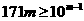 .
.
当 m = 4时,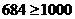 不成立.而
不成立.而 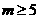 ,更不成立.因此,所有的幸运数都是三位数,由100a + 10b
+ c = 19a + 19b + 19c,知 9a = b + 2c.
,更不成立.因此,所有的幸运数都是三位数,由100a + 10b
+ c = 19a + 19b + 19c,知 9a = b + 2c.
当 a = 1时,可得 (b,c) = (1,4),(3,3),(5,2),(7,1),(9,0).
当 a = 2时,可得 (b,c) = (0,9),(2,8),(4,7),(6,6),(8,5).
当 a = 3时,可得 (b,c) = (9,9).
当 a > 3时,无解.
所以共有 11 个幸运数: 114, 133, 152, 171, 190, 209, 228, 247, 266, 285 和 399.
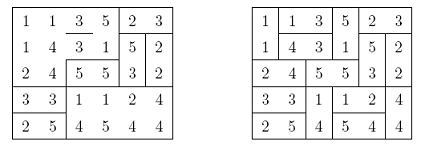
4. 一片骨牌是由两个单位正方形以边对边相连接而成,在每个正方形内标记上数字1、2、3、4或5,所以我们共可得标号为11,12,13,14,15,22,23,24,25,33,34,35,44,45,55的15片不同的骨牌.将这15片骨牌排成一个如图的5×6的长方形,每片骨牌的边界已经擦除,请试着把这些骨牌的边界重新画出来.

解答:首先,注意到编号为55的骨牌一定是在矩形的中心,而编号22的骨牌只能是在右边界处.此时,右上角编号为3的骨牌必与右侧的2一起组成编号为23的骨牌..所以,右下角的2只能与5一起组成编号为25的骨牌,而这个2上面的3只能组成33骨牌..所以,可在图中,把剩下的33、23对之间用一条线分隔.第三行的3只能与其上的5组成35编号的骨牌.如左图.
这时,第一行的5不能与其左侧的3组成35编号的骨牌,只能与其下的1组成编号为15的骨牌.这使得左侧只能为13、34编号的骨牌,这样,左上角的骨牌为11和24.
在右下角,必须出现编号为12的骨牌,此时,其余的骨牌也就确定了.
3.
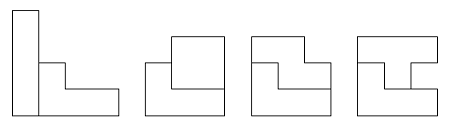
 四个单位正方形以边对边相连接而成,可以拼成如图五种不同的形状.用一片“L”形(图中第一个)分别与其余四个中的一片拼成轴对称图形,请绘出所有可能之组合.
四个单位正方形以边对边相连接而成,可以拼成如图五种不同的形状.用一片“L”形(图中第一个)分别与其余四个中的一片拼成轴对称图形,请绘出所有可能之组合.
解答:
2. 一个三角形可被剖分成两个等腰三角形,原三角形的一个内角为36˚,求原三角形最大内角的所有可能值.
解答:不妨设B=36˚ .
(1)若剖分线不过点B.不妨设剖分线为AD,此时△BAD是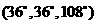 或者
或者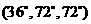 的三角形.
的三角形.
若△BAD是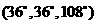 的三角形,则△CAD或者是
的三角形,则△CAD或者是 第一个图,或者是
第一个图,或者是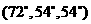 第二个图,或者
第二个图,或者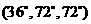 第三、四个图.
第三、四个图.

(2) 若剖分线过点B.不妨设为BE,则△CBE必定是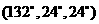 ,△ABE是
,△ABE是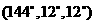 的三角形.
的三角形.
所以原三角形的最大内角可能是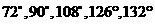 .
.
1. 老师说:“要在一个三边长为2,2,2x的三角形内部放置一个尽可能大的圆,则正实数x的值该是多少?”
学生A说:“我想x=1.”
学生B说:“我认为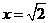 .”
.”
学生C说:“你们回答都不对!”
他们三人谁的回答是正确的?为什么?
解答:一方面三角形的面积=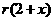 ;另一方面,该三角形底边上的高为
;另一方面,该三角形底边上的高为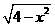 ,所以三角形面积
,所以三角形面积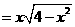 .可得
.可得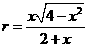 .
.
当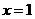 时,
时,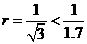 ; 当
; 当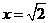 时,
时,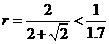 .
.
取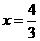 ,则
,则 ,所以
,所以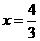 是一个更好的选择.所以学生C的回答正确.
是一个更好的选择.所以学生C的回答正确.
注:当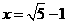 时,可取到r的最大值
时,可取到r的最大值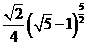 .
.
16.数列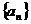 为等和数列(任意相邻的两项之和为一常数的数列称为等和数列),
为等和数列(任意相邻的两项之和为一常数的数列称为等和数列), ,
, ,请设计算法流程图,输出该数列的前50项及这50项的和,并用基本语句描述这个算法.
,请设计算法流程图,输出该数列的前50项及这50项的和,并用基本语句描述这个算法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com